Related Research Articles

Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century.
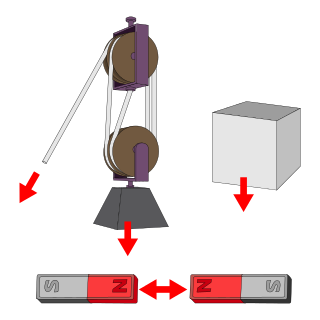
In physics, a force is any interaction that, when unopposed, will change the motion of an object. A force can cause an object with mass to change its velocity, i.e., to accelerate. Force can also be described intuitively as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol F.

In mathematics, a tensor is an algebraic object that describes a (multilinear) relationship between sets of algebraic objects related to a vector space. Objects that tensors may map between include vectors and scalars, and even other tensors. Tensors can take several different forms – for example: scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system.
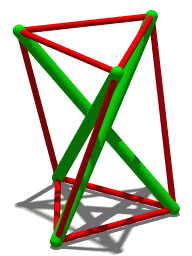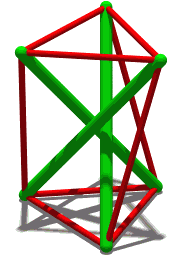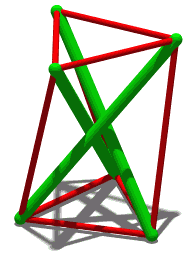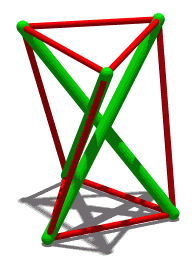
Tensegrity, tensional integrity or floating compression is a structural principle based on a system of isolated components under compression inside a network of continuous tension, and arranged in such a way that the compressed members do not touch each other while the prestressed tensioned members delineate the system spatially.

Biomechanics is the study of the structure, function and motion of the mechanical aspects of biological systems, at any level from whole organisms to organs, cells and cell organelles, using the methods of mechanics. Biomechanics is a branch of biophysics.

In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each particle gets pushed against by all the surrounding particles. The container walls and the pressure-inducing surface push against them in (Newtonian) reaction. These macroscopic forces are actually the net result of a very large number of intermolecular forces and collisions between the particles in those molecules. Stress is frequently represented by a lowercase Greek letter sigma (σ).
Strength of materials, also called mechanics of materials, deals with the behavior of solid objects subject to stresses and strains. The complete theory began with the consideration of the behavior of one and two dimensional members of structures, whose states of stress can be approximated as two dimensional, and was then generalized to three dimensions to develop a more complete theory of the elastic and plastic behavior of materials. An important founding pioneer in mechanics of materials was Stephen Timoshenko.
This is a glossary of tensor theory. For expositions of tensor theory from different points of view, see:
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.
Stress–strain analysis is an engineering discipline that uses many methods to determine the stresses and strains in materials and structures subjected to forces. In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material.

In structural engineering, buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled. Euler's critical load and Johnson's parabolic formula are used to determine the buckling stress in slender columns.
In mathematics, mathematical physics, and theoretical physics, the spin tensor is a quantity used to describe the rotational motion of particles in spacetime. The tensor has application in general relativity and special relativity, as well as quantum mechanics, relativistic quantum mechanics, and quantum field theory.
A scalar or scalar quantity in physics is one that can be described by a single element of a number field such as a real number, often accompanied by units of measurement. A scalar is usually said to be a physical quantity that only has magnitude, possibly a sign, and no other characteristics. This is in contrast to vectors, tensors, etc. which are described by several numbers that characterize their magnitude, direction, and so on.
A mechanician is an engineer or a scientist working in the field of mechanics, or in a related or sub-field: engineering or computational mechanics, applied mechanics, geomechanics, biomechanics, and mechanics of materials. Names other than mechanician have been used occasionally, such as mechaniker and mechanicist.
This is an alphabetical list of articles pertaining specifically to Engineering Science and Mechanics (ESM). For a broad overview of engineering, please see Engineering. For biographies please see List of engineers and Mechanicians.

The mathematics of general relativity are complex. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.

In physics, a field is a physical quantity, represented by a number or tensor, that has a value for each point in space and time. For example, on a weather map, the surface temperature is described by assigning a number to each point on the map; the temperature can be considered at a certain point in time or over some interval of time, to study the dynamics of temperature change. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, would be an example of a vector field, i.e. a 1-dimensional tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, and the full description of electrodynamics can be formulated in terms of two interacting vector fields at each point in space-time, or as a single-rank 2-tensor field theory.
Johannes Ferdinand "Hans" Besseling was professor emeritus of Engineering Mechanics at the Delft University of Technology, worked in the field of the application of solid mechanics to the analysis of structures; constitutive equations for the mathematical description of material behaviour. His specialities are finite element methods, continuum thermodynamics, creep and plasticity of metals.
Henry Louis Langhaar was a mathematician, engineer, researcher, educator, and author in the field of engineering mechanics. In 1978, he retired as Professor Emeritus, after 31 years in the Department of Theoretical & Applied Mechanics (TAM) at the University of Illinois at Urbana-Champaign.
Variational Asymptotic Method (VAM) is a powerful mathematical approach to simplify the process of finding stationary points for a described functional by taking an advantage of small parameters. VAM is the synergy of variational principles and asymptotic approaches, variational principles are applied to the defined functional as well as the asymptotes are applied to the same functional instead of applying on differential equations due to its less prone to errors. This methodology is applicable for whole range of physics problems, where the problem has to be defined in a variational form and should be able to identify the small parameters within the problem definition. In other words, VAM can be applicable where the functional is so complex in determining the stationary points either by analytical or by computationally expensive numerical analysis with an advantage of small parameters. Thus, approximate stationary points in the functional can be utilized to obtain the original functional.
References
- ↑ Danielson, D.A. (2003). Vectors and Tensors in Engineering and Physics, 2nd Edition. CRC Press. pp. 1–282. ISBN 9780813340807.