Uninterpreted function

Last updated

In mathematical logic, an uninterpreted function [1] or function symbol [2] is one that has no other property than its name and n-ary form. Function symbols are used, together with constants and variables, to form terms.

Contents

The theory of uninterpreted functions is also sometimes called the free theory, because it is freely generated, and thus a free object, or the empty theory, being the theory having an empty set of sentences (in analogy to an initial algebra). Theories with a non-empty set of equations are known as equational theories. The satisfiability problem for free theories is solved by syntactic unification; algorithms for the latter are used by interpreters for various computer languages, such as Prolog. Syntactic unification is also used in algorithms for the satisfiability problem for certain other equational theories, see Unification (computer science).

Example

As an example of uninterpreted functions for SMT-LIB, if this input is given to an SMT solver:

(declare-fun f (Int) Int) (assert (= (f 10) 1))

the SMT solver would return "This input is satisfiable". That happens because f is an uninterpreted function (i.e., all that is known about f is its signature), so it is possible that f(10) = 1. But by applying the input below:

(declare-fun f (Int) Int) (assert (= (f 10) 1)) (assert (= (f 10) 42))

the SMT solver would return "This input is unsatisfiable". That happens because f, being a function, can never return different values for the same input.

Discussion

The decision problem for free theories is particularly important, because many theories can be reduced by it. [3]

Free theories can be solved by searching for common subexpressions to form the congruence closure.[ clarification needed ] Solvers include satisfiability modulo theories solvers.

See also

Notes

    Related Research Articles

    Automated theorem proving is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major motivating factor for the development of computer science.

    In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

    The P versus NP problem is a major unsolved problem in theoretical computer science. Informally, it asks whether every problem whose solution can be quickly verified can also be quickly solved.

    In logic and computer science, specifically automated reasoning, unification is an algorithmic process of solving equations between symbolic expressions, each of the form Left-hand side = Right-hand side. For example, using x,y,z as variables, and taking f to be an uninterpreted function, the singleton equation set { f(1,y) = f(x,2) } is a syntactic first-order unification problem that has the substitution { x ↦ 1, y ↦ 2 } as its only solution.

    In computer science, declarative programming is a programming paradigm—a style of building the structure and elements of computer programs—that expresses the logic of a computation without describing its control flow.

    Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint satisfaction methods. CSPs are the subject of research in both artificial intelligence and operations research, since the regularity in their formulation provides a common basis to analyze and solve problems of many seemingly unrelated families. CSPs often exhibit high complexity, requiring a combination of heuristics and combinatorial search methods to be solved in a reasonable time. Constraint programming (CP) is the field of research that specifically focuses on tackling these kinds of problems. Additionally, the Boolean satisfiability problem (SAT), satisfiability modulo theories (SMT), mixed integer programming (MIP) and answer set programming (ASP) are all fields of research focusing on the resolution of particular forms of the constraint satisfaction problem.

    Theoretical computer science is a subfield of computer science and mathematics that focuses on the abstract and mathematical foundations of computation.

    In computer science, program synthesis is the task to construct a program that provably satisfies a given high-level formal specification. In contrast to program verification, the program is to be constructed rather than given; however, both fields make use of formal proof techniques, and both comprise approaches of different degrees of automation. In contrast to automatic programming techniques, specifications in program synthesis are usually non-algorithmic statements in an appropriate logical calculus.

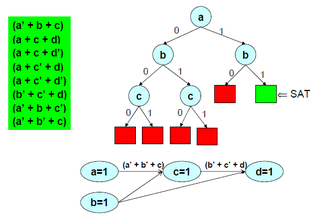
    <span class="mw-page-title-main">DPLL algorithm</span> Type of search algorithm

    In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.

    In computer science, separation logic is an extension of Hoare logic, a way of reasoning about programs. It was developed by John C. Reynolds, Peter O'Hearn, Samin Ishtiaq and Hongseok Yang, drawing upon early work by Rod Burstall. The assertion language of separation logic is a special case of the logic of bunched implications (BI). A CACM review article by O'Hearn charts developments in the subject to early 2019.

    In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.

    Logic optimization is a process of finding an equivalent representation of the specified logic circuit under one or more specified constraints. This process is a part of a logic synthesis applied in digital electronics and integrated circuit design.

    In computer science and formal methods, a SAT solver is a computer program which aims to solve the Boolean satisfiability problem. On input a formula over Boolean variables, such as "(x or y) and (x or not y)", a SAT solver outputs whether the formula is satisfiable, meaning that there are possible values of x and y which make the formula true, or unsatisfiable, meaning that there are no such values of x and y. In this case, the formula is satisfiable when x is true, so the solver should return "satisfiable". Since the introduction of algorithms for SAT in the 1960s, modern SAT solvers have grown into complex software artifacts involving a large number of heuristics and program optimizations to work efficiently.

    A solver is a piece of mathematical software, possibly in the form of a stand-alone computer program or as a software library, that 'solves' a mathematical problem. A solver takes problem descriptions in some sort of generic form and calculates their solution. In a solver, the emphasis is on creating a program or library that can easily be applied to other problems of similar type.

    In mathematical logic, a formula is satisfiable if it is true under some assignment of values to its variables. For example, the formula is satisfiable because it is true when and , while the formula is not satisfiable over the integers. The dual concept to satisfiability is validity; a formula is valid if every assignment of values to its variables makes the formula true. For example, is valid over the integers, but is not.

    In mathematical logic, computational complexity theory, and computer science, the existential theory of the reals is the set of all true sentences of the form where the variables are interpreted as having real number values, and where is a quantifier-free formula involving equalities and inequalities of real polynomials. A sentence of this form is true if it is possible to find values for all of the variables that, when substituted into formula , make it become true.

    Dis-unification, in computer science and logic, is an algorithmic process of solving inequations between symbolic expressions.

    In computer science, DPLL(T) is a framework for determining the satisfiability of SMT problems. The algorithm extends the original SAT-solving DPLL algorithm with the ability to reason about an arbitrary theory T. At a high level, the algorithm works by transforming an SMT problem into a SAT formula where atoms are replaced with Boolean variables. The algorithm repeatedly finds a satisfying valuation for the SAT problem, consults a theory solver to check consistency under the domain-specific theory, and then (if a contradiction is found) refines the SAT formula with this information.

    Z3, also known as the Z3 Theorem Prover, is a satisfiability modulo theories (SMT) solver developed by Microsoft.

    <span class="mw-page-title-main">Ofer Strichman</span>

    Ofer Strichman is a professor of computational logic and computer science at the Davidson Industrial Engineering and Management, Technion – Israel Institute of Technology. He holds the Joseph Gruenblat chair in production engineering.

    References

    1. ↑ Bryant, Randal E.; Lahiri, Shuvendu K.; Seshia, Sanjit A. (2002). "Modeling and Verifying Systems Using a Logic of Counter Arithmetic with Lambda Expressions and Uninterpreted Functions" (PDF). Computer Aided Verification. Lecture Notes in Computer Science. Vol. 2404. pp. 78–92. doi:10.1007/3-540-45657-0_7. ISBN   978-3-540-43997-4. S2CID   9471360.
    2. ↑ Baader, Franz; Nipkow, Tobias (1999). Term Rewriting and All That. Cambridge University Press. p. 34. ISBN   978-0-521-77920-3.
    3. ↑ de Moura, Leonardo; Bjørner, Nikolaj (2009). Formal methods : foundations and applications : 12th Brazilian Symposium on Formal Methods, SBMF 2009, Gramado, Brazil, August 19-21, 2009 : revised selected papers (PDF). Berlin: Springer. ISBN   978-3-642-10452-7.
    This page is based on this Wikipedia article
    Text is available under the CC BY-SA 4.0 license; additional terms may apply.
    Images, videos and audio are available under their respective licenses.