In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".
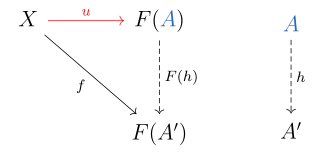
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,

An exact sequence is a sequence of morphisms between objects such that the image of one morphism equals the kernel of the next.
In mathematics, a direct limit is a way to construct a object from many objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms between those smaller objects. The direct limit of the objects , where ranges over some directed set , is denoted by . This notation suppresses the system of homomorphisms; however, the limit depends on the system of homomorphisms.
In mathematics, specifically category theory, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and arrows.
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices.
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category: indeed, every small abelian category can be embedded in Ab.
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
In mathematics, in the area of category theory, a forgetful functor 'forgets' or drops some or all of the input's structure or properties 'before' mapping to the output. For an algebraic structure of a given signature, this may be expressed by curtailing the signature: the new signature is an edited form of the old one. If the signature is left as an empty list, the functor is simply to take the underlying set of a structure. Because many structures in mathematics consist of a set with an additional added structure, a forgetful functor that maps to the underlying set is the most common case.
In category theory, a faithful functor is a functor that is injective on hom-sets, and a full functor is surjective on hom-sets. A functor that has both properties is called a fully faithful functor.
In mathematics, the homotopy category is a category built from the category of topological spaces which in a sense identifies two spaces that have the same shape. The phrase is in fact used for two different categories, as discussed below.
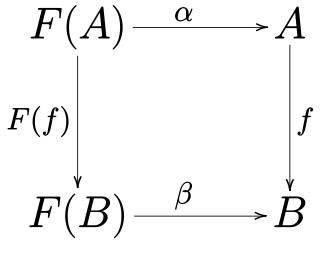
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.
This is a glossary of properties and concepts in category theory in mathematics.
In algebraic geometry, a morphism of schemes generalizes a morphism of algebraic varieties just as a scheme generalizes an algebraic variety. It is, by definition, a morphism in the category of schemes.
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms. Like many categories in mathematics, the category of rings is large, meaning that the class of all rings is proper.
In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.













