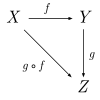Definition
A category C consists of two classes, one of objects and the other of morphisms. There are two objects that are associated to every morphism, the source and the target. A morphismffromXtoY is a morphism with source X and target Y; it is commonly written as f : X → Y or XY the latter form being better suited for commutative diagrams.
For many common categories, an object is a set (often with some additional structure) and a morphism is a function from an object to another object. Therefore, the source and the target of a morphism are often called domain and codomain respectively.
Morphisms are equipped with a partial binary operation, called composition (partial because the composition is not necessarily defined over every pair of morphisms of a category). The composition of two morphisms f and g is defined precisely when the target of f is the source of g, and is denoted g ∘ f (or sometimes simply gf). The source of g ∘ f is the source of f, and the target of g ∘ f is the target of g. The composition satisfies two axioms:
- Identity
- For every object X, there exists a morphism idX : X → X called the identity morphism on X, such that for every morphism f : A → B we have idB ∘ f = f = f ∘ idA.
- Associativity
- h ∘ (g ∘ f) = (h ∘ g) ∘ f whenever all the compositions are defined, i.e. when the target of f is the source of g, and the target of g is the source of h.
For a concrete category (a category in which the objects are sets, possibly with additional structure, and the morphisms are structure-preserving functions), the identity morphism is just the identity function, and composition is just ordinary composition of functions.
The composition of morphisms is often represented by a commutative diagram. For example,
The collection of all morphisms from X to Y is denoted HomC(X, Y) or simply Hom(X, Y) and called the hom-set between X and Y. Some authors write MorC(X, Y), Mor(X, Y) or C(X, Y). The term hom-set is something of a misnomer, as the collection of morphisms is not required to be a set; a category where Hom(X, Y) is a set for all objects X and Y is called locally small. Because hom-sets may not be sets, some people prefer to use the term "hom-class".
The domain and codomain are in fact part of the information determining a morphism. For example, in the category of sets, where morphisms are functions, two functions may be identical as sets of ordered pairs, while having different codomains. The two functions are distinct from the viewpoint of category theory. Many authors require that the hom-classes Hom(X, Y) be disjoint. In practice, this is not a problem because if this disjointness does not hold, it can be assured by appending the domain and codomain to the morphisms (say, as the second and third components of an ordered triple).