In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the ancient Greek language: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same".
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation.

In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In mathematics, in particular abstract algebra, a graded ring is a ring that is a direct sum of abelian groups such that . The index set is usually the set of nonnegative integers or the set of integers, but can be any monoid. The direct sum decomposition is usually referred to as gradation or grading.
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure. It also has a formulation in terms of category theory, although this is in yet more abstract terms. Examples include free groups, tensor algebras, or free lattices. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure.
In mathematics, the Eckmann–Hilton argument is an argument about two monoid structures on a set where one is a homomorphism for the other. Given this, the structures can be shown to coincide, and the resulting monoid demonstrated to be commutative. This can then be used to prove the commutativity of the higher homotopy groups. The principle is named after Beno Eckmann and Peter Hilton, who used it in a 1962 paper.
In abstract algebra, the free monoid on a set is the monoid whose elements are all the finite sequences of zero or more elements from that set, with string concatenation as the monoid operation and with the unique sequence of zero elements, often called the empty string and denoted by ε or λ, as the identity element. The free monoid on a set A is usually denoted A∗. The free semigroup on A is the subsemigroup of A∗ containing all elements except the empty string. It is usually denoted A+.
In algebra and theoretical computer science, an action or act of a semigroup on a set is a rule which associates to each element of the semigroup a transformation of the set in such a way that the product of two elements of the semigroup is associated with the composite of the two corresponding transformations. The terminology conveys the idea that the elements of the semigroup are acting as transformations of the set. From an algebraic perspective, a semigroup action is a generalization of the notion of a group action in group theory. From the computer science point of view, semigroup actions are closely related to automata: the set models the state of the automaton and the action models transformations of that state in response to inputs.
This is a glossary of properties and concepts in category theory in mathematics.
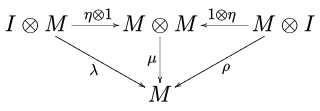
In category theory, a monoid in a monoidal category is an object M together with two morphisms
In category theory, a branch of mathematics, a PROP is a symmetric strict monoidal category whose objects are the natural numbers n identified with the finite sets and whose tensor product is given on objects by the addition on numbers. Because of “symmetric”, for each n, the symmetric group on n letters is given as a subgroup of the automorphism group of n. The name PROP is an abbreviation of "PROduct and Permutation category".
In mathematics and theoretical computer science, a semiautomaton is a deterministic finite automaton having inputs but no output. It consists of a set Q of states, a set Σ called the input alphabet, and a function T: Q × Σ → Q called the transition function.
In mathematics and computer science, a history monoid is a way of representing the histories of concurrently running computer processes as a collection of strings, each string representing the individual history of a process. The history monoid provides a set of synchronization primitives for providing rendezvous points between a set of independently executing processes or threads.
In category theory, a branch of mathematics, the center is a variant of the notion of the center of a monoid, group, or ring to a category.
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French–English pun, Fun. The name "field with one element" and the notation F1 are only suggestive, as there is no field with one element in classical abstract algebra. Instead, F1 refers to the idea that there should be a way to replace sets and operations, the traditional building blocks for abstract algebra, with other, more flexible objects. While there is still no field with a single element in these theories, there is a field-like object whose characteristic is one.
In mathematics, the plactic monoid is the monoid of all words in the alphabet of positive integers modulo Knuth equivalence. Its elements can be identified with semistandard Young tableaux. It was discovered by Donald Knuth (1970), using an operation given by Craige Schensted (1961) in his study of the longest increasing subsequence of a permutation.
In mathematics, a highly structured ring spectrum or -ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an -ring is called an -ring. While originally motivated by questions of geometric topology and bundle theory, they are today most often used in stable homotopy theory.
In arithmetic geometry, a Frobenioid is a category with some extra structure that generalizes the theory of line bundles on models of finite extensions of global fields. Frobenioids were introduced by Shinichi Mochizuki (2008). The word "Frobenioid" is a portmanteau of Frobenius and monoid, as certain Frobenius morphisms between Frobenioids are analogues of the usual Frobenius morphism, and some of the simplest examples of Frobenioids are essentially monoids.




