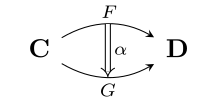In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. [1] It is said that commutative diagrams play the role in category theory that equations play in algebra. [2]
A commutative diagram often consists of three parts:
In algebra texts, the type of morphism can be denoted with different arrow usages:
The meanings of different arrows are not entirely standardized: the arrows used for monomorphisms, epimorphisms, and isomorphisms are also used for injections, surjections, and bijections, as well as the cofibrations, fibrations, and weak equivalences in a model category.
Commutativity makes sense for a polygon of any finite number of sides (including just 1 or 2), and a diagram is commutative if every polygonal subdiagram is commutative.
Note that a diagram may be non-commutative, i.e., the composition of different paths in the diagram may not give the same result.
In the left diagram, which expresses the first isomorphism theorem, commutativity of the triangle means that . In the right diagram, commutativity of the square means .
 |  |
In order for the diagram below to commute, three equalities must be satisfied:
Here, since the first equality follows from the last two, it suffices to show that (2) and (3) are true in order for the diagram to commute. However, since equality (3) generally does not follow from the other two, it is generally not enough to have only equalities (1) and (2) if one were to show that the diagram commutes.
 |
Diagram chasing (also called diagrammatic search) is a method of mathematical proof used especially in homological algebra, where one establishes a property of some morphism by tracing the elements of a commutative diagram. A proof by diagram chasing typically involves the formal use of the properties of the diagram, such as injective or surjective maps, or exact sequences. [5] A syllogism is constructed, for which the graphical display of the diagram is just a visual aid. It follows that one ends up "chasing" elements around the diagram, until the desired element or result is constructed or verified.
Examples of proofs by diagram chasing include those typically given for the five lemma, the snake lemma, the zig-zag lemma, and the nine lemma.
In higher category theory, one considers not only objects and arrows, but arrows between the arrows, arrows between arrows between arrows, and so on ad infinitum. For example, the category of small categories Cat is naturally a 2-category, with functors as its arrows and natural transformations as the arrows between functors. In this setting, commutative diagrams may include these higher arrows as well, which are often depicted in the following style: . For example, the following (somewhat trivial) diagram depicts two categories C and D, together with two functors F, G : C → D and a natural transformation α : F ⇒ G:
There are two kinds of composition in a 2-category (called vertical composition and horizontal composition), and they may also be depicted via pasting diagrams (see 2-category#Definition for examples).
A commutative diagram in a category C can be interpreted as a functor from an index category J to C; one calls the functor a diagram.
More formally, a commutative diagram is a visualization of a diagram indexed by a poset category. Such a diagram typically includes:
Conversely, given a commutative diagram, it defines a poset category, where:
However, not every diagram commutes (the notion of diagram strictly generalizes commutative diagram). As a simple example, the diagram of a single object with an endomorphism (), or with two parallel arrows (, that is, , sometimes called the free quiver), as used in the definition of equalizer need not commute. Further, diagrams may be messy or impossible to draw, when the number of objects or morphisms is large (or even infinite).
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in almost all areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality.
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In mathematics, the Yoneda lemma is a fundamental result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties.
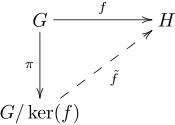
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation .
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In mathematics, especially homological algebra and other applications of abelian category theory, the five lemma is an important and widely used lemma about commutative diagrams. The five lemma is not only valid for abelian categories but also works in the category of groups, for example.
An exact sequence is a sequence of morphisms between objects such that the image of one morphism equals the kernel of the next.
Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert.
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the Cartesian product of sets, the direct product of groups or rings, and the product of topological spaces. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.
In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products within a given category.
The following outline is provided as an overview of and guide to category theory, the area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows, where these collections satisfy certain basic conditions. Many significant areas of mathematics can be formalised as categories, and the use of category theory allows many intricate and subtle mathematical results in these fields to be stated, and proved, in a much simpler way than without the use of categories.
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain. The pullback is written
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms ('arrows') called 'weak equivalences', 'fibrations' and 'cofibrations' satisfying certain axioms relating them. These abstract from the category of topological spaces or of chain complexes. The concept was introduced by Daniel G. Quillen.
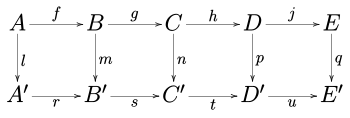
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms that also need indexing. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.
In mathematics, a morphism is a concept of category theory that generalizes structure-preserving maps such as homomorphism between algebraic structures, functions from a set to another set, and continuous functions between topological spaces. Although many examples of morphisms are structure-preserving maps, morphisms need not to be maps, but they can be composed in a way that is similar to function composition.
|  | |||||||||||||||||
| ||||||||||||||||||
