In mathematics and computer science, currying is the technique of translating a function that takes multiple arguments into a sequence of families of functions, each taking a single argument.
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
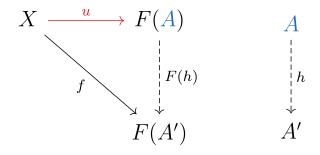
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In mathematics, the Yoneda lemma is a fundamental result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.
In mathematics, the Ext functors are the derived functors of the Hom functor. Along with the Tor functor, Ext is one of the core concepts of homological algebra, in which ideas from algebraic topology are used to define invariants of algebraic structures. The cohomology of groups, Lie algebras, and associative algebras can all be defined in terms of Ext. The name comes from the fact that the first Ext group Ext1 classifies extensions of one module by another.
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain. The pullback is written
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
In mathematics, especially in category theory, a closed monoidal category is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.
In mathematics, a triangulated category is a category with the additional structure of a "translation functor" and a class of "exact triangles". Prominent examples are the derived category of an abelian category, as well as the stable homotopy category. The exact triangles generalize the short exact sequences in an abelian category, as well as fiber sequences and cofiber sequences in topology.
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined. As an example, for each topological space there is the category of vector bundles on the space, and for every continuous map from a topological space X to another topological space Y is associated the pullback functor taking bundles on Y to bundles on X. Fibred categories formalise the system consisting of these categories and inverse image functors. Similar setups appear in various guises in mathematics, in particular in algebraic geometry, which is the context in which fibred categories originally appeared. Fibered categories are used to define stacks, which are fibered categories with "descent". Fibrations also play an important role in categorical semantics of type theory, and in particular that of dependent type theories.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
In category theory, a branch of mathematics, a presheaf on a category is a functor . If is the poset of open sets in a topological space, interpreted as a category, then one recovers the usual notion of presheaf on a topological space.
In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.


























