Closed monoidal category

Last updated September 18, 2023

In mathematics, especially in category theory, a closed monoidal category (or a monoidal closed category) is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.

A classic example is the category of sets, Set, where the monoidal product of sets $A$ and $B$ is the usual cartesian product $A\times B$ , and the internal Hom $B^{A}$ is the set of functions from $A$ to $B$ . A non-cartesian example is the category of vector spaces, K-Vect, over a field $K$ . Here the monoidal product is the usual tensor product of vector spaces, and the internal Hom is the vector space of linear maps from one vector space to another.

The internal language of closed symmetric monoidal categories is linear logic and the type system is the linear type system. Many examples of closed monoidal categories are symmetric. However, this need not always be the case, as non-symmetric monoidal categories can be encountered in category-theoretic formulations of linguistics; roughly speaking, this is because word-order in natural language matters.

Definition

A closed monoidal category is a monoidal category ${\mathcal {C}}$ such that for every object $B$ the functor given by right tensoring with $B$

A\mapsto A\otimes B

has a right adjoint, written

A\mapsto (B\Rightarrow A).

This means that there exists a bijection, called 'currying', between the Hom-sets

{\text{Hom}}_{\mathcal {C}}(A\otimes B,C)\cong {\text{Hom}}_{\mathcal {C}}(A,B\Rightarrow C)

that is natural in both A and C. In a different, but common notation, one would say that the functor

-\otimes B:{\mathcal {C}}\to {\mathcal {C}}

has a right adjoint

[B,-]:{\mathcal {C}}\to {\mathcal {C}}

Equivalently, a closed monoidal category ${\mathcal {C}}$ is a category equipped, for every two objects A and B, with

an object $A\Rightarrow B$ ,
a morphism $\mathrm {eval} _{A,B}:(A\Rightarrow B)\otimes A\to B$ ,

satisfying the following universal property: for every morphism

f:X\otimes A\to B

there exists a unique morphism

h:X\to A\Rightarrow B

such that

f=\mathrm {eval} _{A,B}\circ (h\otimes \mathrm {id} _{A}).

It can be shown^{[ citation needed ]} that this construction defines a functor ${\displaystyle \Rightarrow$ . This functor is called the internal Hom functor, and the object $A\Rightarrow B$ is called the internal Hom of $A$ and $B$ . Many other notations are in common use for the internal Hom. When the tensor product on ${\mathcal {C}}$ is the cartesian product, the usual notation is $B^{A}$ and this object is called the exponential object.

Biclosed and symmetric categories

Strictly speaking, we have defined a right closed monoidal category, since we required that right tensoring with any object $A$ has a right adjoint. In a left closed monoidal category, we instead demand that the functor of left tensoring with any object $A$

B\mapsto A\otimes B

have a right adjoint

B\mapsto (B\Leftarrow A)

A biclosed monoidal category is a monoidal category that is both left and right closed.

A symmetric monoidal category is left closed if and only if it is right closed. Thus we may safely speak of a 'symmetric monoidal closed category' without specifying whether it is left or right closed. In fact, the same is true more generally for braided monoidal categories: since the braiding makes $A\otimes B$ naturally isomorphic to $B\otimes A$ , the distinction between tensoring on the left and tensoring on the right becomes immaterial, so every right closed braided monoidal category becomes left closed in a canonical way, and vice versa.

We have described closed monoidal categories as monoidal categories with an extra property. One can equivalently define a closed monoidal category to be a closed category with an extra property. Namely, we can demand the existence of a tensor product that is left adjoint to the internal Hom functor. In this approach, closed monoidal categories are also called monoidal closed categories.^{[ citation needed ]}

Examples

Every cartesian closed category is a symmetric, monoidal closed category, when the monoidal structure is the cartesian product structure. The internal Hom functor is given by the exponential object $B^{A}$ $Closed monoidal category$ .
- In particular, the category of sets, Set, is a symmetric, closed monoidal category. Here the internal Hom $A\Rightarrow B$ is just the set of functions from $A$ to $B$ .
The category of modules, R-Mod over a commutative ring R is a non-cartesian, symmetric, monoidal closed category. The monoidal product is given by the tensor product of modules and the internal Hom $M\Rightarrow N$ $Closed monoidal category$ is given by the space of R-linear maps $\operatorname {Hom} _{R}(M,N)$ $Closed monoidal category$ with its natural R-module structure.
- In particular, the category of vector spaces over a field $K$ is a symmetric, closed monoidal category.
- Abelian groups can be regarded as Z-modules, so the category of abelian groups is also a symmetric, closed monoidal category.
A symmetric compact closed category is a symmetric monoidal closed category in which the internal Hom functor $A\Rightarrow B$ is given by $A^{*}\otimes B$ . The canonical example is the category of finite-dimensional vector spaces, FdVect.

Counterexamples

The category of rings is a symmetric, monoidal category under the tensor product of rings, with $\mathbb {Z}$ serving as the unit object. This category is not closed. If it were, there would be exactly one homomorphism between any pair of rings: $\operatorname {Hom} (R,S)\cong \operatorname {Hom} (\mathbb {Z} \otimes R,S)\cong \operatorname {Hom} (\mathbb {Z} ,R\Rightarrow S)\cong \{\bullet \}$ . The same holds for the category of R-algebras over a commutative ring R.

Related Research Articles

In mathematics and computer science, currying is the technique of translating the evaluation of a function that takes multiple arguments into evaluating a sequence of functions, each with a single argument. For example, currying a function $that takes three arguments creates a nested unary function, so that the code$

In mathematics, the tensor product $of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted$

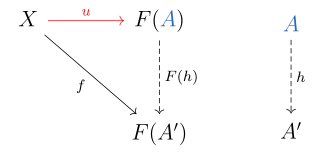
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.

In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.

In mathematics, a monoidal category is a category $equipped with a bifunctor$

In mathematics, particularly homological algebra, an exact functor is a functor that preserves short exact sequences. Exact functors are convenient for algebraic calculations because they can be directly applied to presentations of objects. Much of the work in homological algebra is designed to cope with functors that fail to be exact, but in ways that can still be controlled.

In mathematics, the symmetric algebra $S (V)$ (also denoted $Sym(V))$ on a vector space $V$ over a field $K$ is a commutative algebra over $K$ that contains $V$ , and is, in some sense, minimal for this property. Here, "minimal" means that $S (V)$ satisfies the following universal property: for every linear map $f$ from $V$ to a commutative algebra $A$ , there is a unique algebra homomorphism $g : S (V) \to A$ such that $f = g \circ i$ , where $i$ is the inclusion map of $V$ in $S (V)$ .

In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.

This is a glossary of properties and concepts in category theory in mathematics.

In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.

In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps. The module construction is analogous to the construction of the tensor product of vector spaces, but can be carried out for a pair of modules over a commutative ring resulting in a third module, and also for a pair of a right-module and a left-module over any ring, with result an abelian group. Tensor products are important in areas of abstract algebra, homological algebra, algebraic topology, algebraic geometry, operator algebras and noncommutative geometry. The universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. The tensor product of an algebra and a module can be used for extension of scalars. For a commutative ring, the tensor product of modules can be iterated to form the tensor algebra of a module, allowing one to define multiplication in the module in a universal way.

In mathematics, a super vector space is a -graded vector space, that is, a vector space over a field $with a given decomposition of subspaces of grade and grade . The study of super vector spaces and their generalizations is sometimes called super linear algebra . These objects find their principal application in theoretical physics where they are used to describe the various algebraic aspects of supersymmetry.$

In category theory, a branch of mathematics, a symmetric monoidal category is a monoidal category such that the tensor product is symmetric. One of the prototypical examples of a symmetric monoidal category is the category of vector spaces over some fixed field k, using the ordinary tensor product of vector spaces.

In mathematics, a *-autonomous category C is a symmetric monoidal closed category equipped with a dualizing object $. The concept is also referred to as Grothendieck—Verdier category in view of its relation to the notion of Verdier duality.$

String diagrams are a formal graphical language for representing morphisms in monoidal categories, or more generally 2-cells in 2-categories. They are a prominent tool in applied category theory. When interpreted in the monoidal category of vector spaces and linear maps with the tensor product, string diagrams are called tensor networks or Penrose graphical notation. This has led to the development of categorical quantum mechanics where the axioms of quantum theory are expressed in the language of monoidal categories.

In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors

In category theory, a branch of mathematics, a dual object is an analogue of a dual vector space from linear algebra for objects in arbitrary monoidal categories. It is only a partial generalization, based upon the categorical properties of duality for finite-dimensional vector spaces. An object admitting a dual is called a dualizable object. In this formalism, infinite-dimensional vector spaces are not dualizable, since the dual vector space V^∗ doesn't satisfy the axioms. Often, an object is dualizable only when it satisfies some finiteness or compactness property.

In category theory, a branch of mathematics, dagger compact categories first appeared in 1989 in the work of Sergio Doplicher and John E. Roberts on the reconstruction of compact topological groups from their category of finite-dimensional continuous unitary representations. They also appeared in the work of John Baez and James Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories, for n = 1 and k = 3. They are a fundamental structure in Samson Abramsky and Bob Coecke's categorical quantum mechanics.

In mathematics, the tensor-hom adjunction is that the tensor product $and hom-functor form an adjoint pair:$

In category theory, a branch of mathematics, the center is a variant of the notion of the center of a monoid, group, or ring to a category.

References

Kelly, G.M. (1982). Basic Concepts of Enriched Category Theory (PDF). London Mathematical Society Lecture Note Series. Vol. 64. Cambridge University Press. ISBN 978-0-521-28702-9. OCLC 1015056596.
Melliès, Paul-André (2009). "Categorical Semantics of Linear Logic" (PDF). Panoramas et Synthèses. 27: 1–197. CiteSeerX 10.1.1.62.5117 .
Closed monoidal category at the nLab

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.