
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality.
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts.
In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.
In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products.
In mathematics, a monoidal category is a category equipped with a bifunctor
In category theory, a branch of mathematics, a monad is a monoid in the category of endofunctors. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes and in functional programming languages, allowing languages with non-mutable states to do things such as simulate for-loops; see Monad.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.
In mathematics, a simplicial set is an object composed of simplices in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. Formally, a simplicial set may be defined as a contravariant functor from the simplex category to the category of sets. Simplicial sets were introduced in 1950 by Samuel Eilenberg and Joseph A. Zilber.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
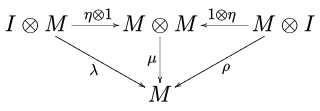
In category theory, a branch of mathematics, a monoid(M, μ, η) in a monoidal category (C, ⊗, I) is an object M together with two morphisms
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
In category theory, a branch of mathematics, a PROP is a symmetric strict monoidal category whose objects are the natural numbers n identified with the finite sets and whose tensor product is given on objects by the addition on numbers. Because of “symmetric”, for each n, the symmetric group on n letters is given as a subgroup of the automorphism group of n. The name PROP is an abbreviation of "PROduct and Permutation category".
In category theory, a branch of mathematics, dagger compact categories first appeared in 1989 in the work of Sergio Doplicher and John E. Roberts on the reconstruction of compact topological groups from their category of finite-dimensional continuous unitary representations. They also appeared in the work of John Baez and James Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories, for n = 1 and k = 3. They are a fundamental structure in Samson Abramsky and Bob Coecke's categorical quantum mechanics.
In mathematics, Kan complexes and Kan fibrations are part of the theory of simplicial sets. Kan fibrations are the fibrations of the standard model category structure on simplicial sets and are therefore of fundamental importance. Kan complexes are the fibrant objects in this model category. The name is in honor of Daniel Kan.
In algebraic geometry and algebraic topology, branches of mathematics, A1homotopy theory or motivic homotopy theory is a way to apply the techniques of algebraic topology, specifically homotopy, to algebraic varieties and, more generally, to schemes. The theory is due to Fabien Morel and Vladimir Voevodsky. The underlying idea is that it should be possible to develop a purely algebraic approach to homotopy theory by replacing the unit interval [0, 1], which is not an algebraic variety, with the affine line A1, which is. The theory has seen spectacular applications such as Voevodsky's construction of the derived category of mixed motives and the proof of the Milnor and Bloch-Kato conjectures.
In mathematics, a Δ-setS, often called a semi-simplicial set, is a combinatorial object that is useful in the construction and triangulation of topological spaces, and also in the computation of related algebraic invariants of such spaces. A Δ-set is somewhat more general than a simplicial complex, yet not quite as general as a simplicial set.
In mathematics, more specifically in homotopy theory, a simplicial presheaf is a presheaf on a site taking values in simplicial sets. Equivalently, a simplicial presheaf is a simplicial object in the category of presheaves on a site. The notion was introduced by A. Joyal in the 1970s. Similarly, a simplicial sheaf on a site is a simplicial object in the category of sheaves on the site.













