Diagram (category theory)

Last updated August 01, 2024

In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms that also need indexing. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.

Definition

Formally, a diagram of type J in a category C is a (covariant) functor

D : J→C.

The category J is called the index category or the scheme of the diagram D; the functor is sometimes called a J-shaped diagram.^[1] The actual objects and morphisms in J are largely irrelevant; only the way in which they are interrelated matters. The diagram D is thought of as indexing a collection of objects and morphisms in C patterned on J.

Although, technically, there is no difference between an individual diagram and a functor or between a scheme and a category, the change in terminology reflects a change in perspective, just as in the set theoretic case: one fixes the index category, and allows the functor (and, secondarily, the target category) to vary.

One is most often interested in the case where the scheme J is a small or even finite category. A diagram is said to be small or finite whenever J is.

A morphism of diagrams of type J in a category C is a natural transformation between functors. One can then interpret the category of diagrams of type J in C as the functor category C^J, and a diagram is then an object in this category.

Examples

Given any object A in C, one has the constant diagram, which is the diagram that maps all objects in J to A, and all morphisms of J to the identity morphism on A. Notationally, one often uses an underbar to denote the constant diagram: thus, for any object $A$ in C, one has the constant diagram ${\underline {A}}$ .
If J is a (small) discrete category, then a diagram of type J is essentially just an indexed family of objects in C (indexed by J). When used in the construction of the limit, the result is the product; for the colimit, one gets the coproduct. So, for example, when J is the discrete category with two objects, the resulting limit is just the binary product.
If J = −1 ← 0 → +1, then a diagram of type J (A ← B → C) is a span, and its colimit is a pushout. If one were to "forget" that the diagram had object B and the two arrows B → A, B → C, the resulting diagram would simply be the discrete category with the two objects A and C, and the colimit would simply be the binary coproduct. Thus, this example shows an important way in which the idea of the diagram generalizes that of the index set in set theory: by including the morphisms B → A, B → C, one discovers additional structure in constructions built from the diagram, structure that would not be evident if one only had an index set with no relations between the objects in the index.
Dual to the above, if J = −1 → 0 ← +1, then a diagram of type J (A → B ← C) is a cospan, and its limit is a pullback.
The index $J=0\rightrightarrows 1$ is called "two parallel morphisms", or sometimes the free quiver or the walking quiver. A diagram of type $J$ $(f,g\colon X\to Y)$ is then a quiver; its limit is an equalizer, and its colimit is a coequalizer.
If J is a poset category, then a diagram of type J is a family of objects D_i together with a unique morphism f_ij : D_i → D_j whenever i ≤ j. If J is directed then a diagram of type J is called a direct system of objects and morphisms. If the diagram is contravariant then it is called an inverse system.

Cones and limits

A cone with vertex N of a diagram D : J → C is a morphism from the constant diagram Δ(N) to D. The constant diagram is the diagram which sends every object of J to an object N of C and every morphism to the identity morphism on N.

The limit of a diagram D is a universal cone to D. That is, a cone through which all other cones uniquely factor. If the limit exists in a category C for all diagrams of type J one obtains a functor

lim : C^J→C

which sends each diagram to its limit.

Dually, the colimit of diagram D is a universal cone from D. If the colimit exists for all diagrams of type J one has a functor

colim : C^J→C

which sends each diagram to its colimit.

The universal functor of a diagram is the diagonal functor; its right adjoint is the limit and its left adjoint is the colimit.^[2] A cone can be thought of as a natural transformation from the diagonal functor to some arbitrary diagram.

Commutative diagrams

Diagrams and functor categories are often visualized by commutative diagrams, particularly if the index category is a finite poset category with few elements: one draws a commutative diagram with a node for every object in the index category, and an arrow for a generating set of morphisms, omitting identity maps and morphisms that can be expressed as compositions. The commutativity corresponds to the uniqueness of a map between two objects in a poset category. Conversely, every commutative diagram represents a diagram (a functor from a poset index category) in this way.

Not every diagram commutes, as not every index category is a poset category: most simply, the diagram of a single object with an endomorphism ( $f\colon X\to X$ ), or with two parallel arrows ( $\bullet \rightrightarrows \bullet$ ; $f,g\colon X\to Y$ ) need not commute. Further, diagrams may be impossible to draw (because they are infinite) or simply messy (because there are too many objects or morphisms); however, schematic commutative diagrams (for subcategories of the index category, or with ellipses, such as for a directed system) are used to clarify such complex diagrams.

Related Research Articles

In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.

In mathematics, the inverse limit is a construction that allows one to "glue together" several related objects, the precise gluing process being specified by morphisms between the objects. Thus, inverse limits can be defined in any category although their existence depends on the category that is considered. They are a special case of the concept of limit in category theory.

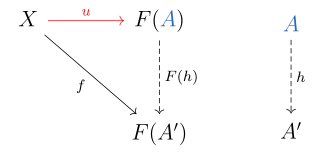
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.

In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.

In category theory, a branch of mathematics, an initial object of a category $C$ is an object $I$ in $C$ such that for every object $X$ in $C$ , there exists precisely one morphism $I \to X$ .

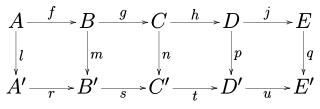
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.

In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the Cartesian product of sets, the direct product of groups or rings, and the product of topological spaces. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.

In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products within a given category.

In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere, although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category".

In mathematics, a triangulated category is a category with the additional structure of a "translation functor" and a class of "exact triangles". Prominent examples are the derived category of an abelian category, as well as the stable homotopy category. The exact triangles generalize the short exact sequences in an abelian category, as well as fiber sequences and cofiber sequences in topology.

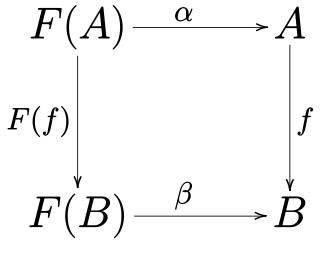
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

This is a glossary of properties and concepts in category theory in mathematics.

Kan extensions are universal constructs in category theory, a branch of mathematics. They are closely related to adjoints, but are also related to limits and ends. They are named after Daniel M. Kan, who constructed certain (Kan) extensions using limits in 1960.

In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.

In category theory, a branch of mathematics, the diagonal functor $is given by, which maps objects as well as morphisms. This functor can be employed to give a succinct alternate description of the product of objects within the category : a product is a universal arrow from to . The arrow comprises the projection maps.$

In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.

In mathematics, derivators are a proposed framework^{pg 190-195} for homological algebra giving a foundation for both abelian and non-abelian homological algebra and various generalizations of it. They were introduced to address the deficiencies of derived categories and provide at the same time a language for homotopical algebra.

In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms. Like many categories in mathematics, the category of rings is large, meaning that the class of all rings is proper.

In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.

In mathematics, especially in algebraic topology, the homotopy limit and colimit^{pg 52} are variants of the notions of limit and colimit extended to the homotopy category $. The main idea is this: if we have a diagram$

References

↑ May, J. P. (1999). A Concise Course in Algebraic Topology (PDF). University of Chicago Press. p. 16. ISBN 0-226-51183-9.
↑ Mac Lane, Saunders; Moerdijk, Ieke (1992). Sheaves in geometry and logic a first introduction to topos theory . New York: Springer-Verlag. pp. 20–23. ISBN 9780387977102.

Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstract and Concrete Categories (PDF). John Wiley & Sons. ISBN 0-471-60922-6. Now available as free on-line edition (4.2MB PDF).
Barr, Michael; Wells, Charles (2002). Toposes, Triples and Theories (PDF). ISBN 0-387-96115-1. Revised and corrected free online version of Grundlehren der mathematischen Wissenschaften (278) Springer-Verlag, 1983).
diagram at the nLab

External links

Diagram Chasing at MathWorld
WildCats is a category theory package for Mathematica. Manipulation and visualization of objects, morphisms, commutative diagrams, categories, functors, natural transformations.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] May, J. P. (1999). A Concise Course in Algebraic Topology (PDF). University of Chicago Press. p. 16. ISBN 0-226-51183-9.

[2] Mac Lane, Saunders; Moerdijk, Ieke (1992). Sheaves in geometry and logic a first introduction to topos theory . New York: Springer-Verlag. pp. 20–23. ISBN 9780387977102.

[1]

[2]