In category theory, a span, roof or correspondence is a generalization of the notion of relation between two objects of a category. When the category has all pullbacks (and satisfies a small number of other conditions), spans can be considered as morphisms in a category of fractions.
The notion of a span is due to Nobuo Yoneda (1954) and Jean Bénabou (1967).
A span is a diagram of type i.e., a diagram of the form .
That is, let Λ be the category (-1 ← 0 → +1). Then a span in a category C is a functor S : Λ → C. This means that a span consists of three objects X, Y and Z of C and morphisms f : X → Y and g : X → Z: it is two maps with common domain.
A cospan K in a category C is a functor K : Λop → C; equivalently, a contravariant functor from Λ to C. That is, a diagram of type i.e., a diagram of the form .
Thus it consists of three objects X, Y and Z of C and morphisms f : Y → X and g : Z → X: it is two maps with common codomain.
The limit of a cospan is a pullback.
An example of a cospan is a cobordism W between two manifolds M and N, where the two maps are the inclusions into W. Note that while cobordisms are cospans, the category of cobordisms is not a "cospan category": it is not the category of all cospans in "the category of manifolds with inclusions on the boundary", but rather a subcategory thereof, as the requirement that M and N form a partition of the boundary of W is a global constraint.
The category nCob of finite-dimensional cobordisms is a dagger compact category. More generally, the category Span(C) of spans on any category C with finite limits is also dagger compact.
In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C that makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.
In mathematics, the Yoneda lemma is a fundamental result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.
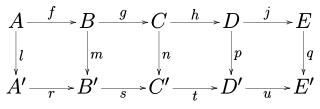
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.
Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert.
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain. The pushout consists of an object P along with two morphisms X → P and Y → P that complete a commutative square with the two given morphisms f and g. In fact, the defining universal property of the pushout essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are and .
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain. The pullback is written
In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequences.
In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories without adjoined products may still have an exponential law.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, specifically in category theory, hom-sets give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms that also need indexing. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.
In category theory, a regular category is a category with finite limits and coequalizers of a pair of morphisms called kernel pairs, satisfying certain exactness conditions. In that way, regular categories recapture many properties of abelian categories, like the existence of images, without requiring additivity. At the same time, regular categories provide a foundation for the study of a fragment of first-order logic, known as regular logic.
In mathematics, especially in algebraic topology, the homotopy limit and colimitpg 52 are variants of the notions of limit and colimit extended to the homotopy category . The main idea is this: if we have a diagram
In category theory and homotopy theory the Burnside category of a finite group G is a category whose objects are finite G-sets and whose morphisms are spans of G-equivariant maps. It is a categorification of the Burnside ring of G.
This is a glossary of properties and concepts in algebraic topology in mathematics.
In mathematics, specifically in category theory, a quasi-abelian category is a pre-abelian category in which the pushout of a kernel along arbitrary morphisms is again a kernel and, dually, the pullback of a cokernel along arbitrary morphisms is again a cokernel.
