Related Research Articles

Alexander Grothendieck, later Alexandre Grothendieck in French, was a German-born French mathematician who became the leading figure in the creation of modern algebraic geometry. His research extended the scope of the field and added elements of commutative algebra, homological algebra, sheaf theory, and category theory to its foundations, while his so-called "relative" perspective led to revolutionary advances in many areas of pure mathematics. He is considered by many to be the greatest mathematician of the twentieth century.
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in almost all areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality.

In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
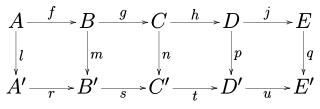
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.
This article gives some very general background to the mathematical idea of topos. This is an aspect of category theory, and has a reputation for being abstruse. The level of abstraction involved cannot be reduced beyond a certain point; but on the other hand context can be given. This is partly in terms of historical development, but also to some extent an explanation of differing attitudes to category theory.
Errett Albert Bishop was an American mathematician known for his work on analysis. He is best known for developing constructive analysis in his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis using "constructivist" methods.

Samuel Eilenberg was a Polish-American mathematician who co-founded category theory and homological algebra.
In mathematics, Grothendieck's Galois theory is an abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry. It provides, in the classical setting of field theory, an alternative perspective to that of Emil Artin based on linear algebra, which became standard from about the 1930s.
In mathematics, abstract nonsense, general abstract nonsense, generalized abstract nonsense, and general nonsense are nonderogatory terms used by mathematicians to describe long, theoretical parts of a proof they skip over when readers are expected to be familiar with them. These terms are mainly used for abstract methods related to category theory and homological algebra. More generally, "abstract nonsense" may refer to a proof that relies on category-theoretic methods, or even to the study of category theory itself.

Francis William Lawvere was an American mathematician known for his work in category theory, topos theory and the philosophy of mathematics.
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory, History of the Theory of Numbers. The L. E. Dickson instructorships at the University of Chicago Department of Mathematics are named after him.
In category theory, a branch of mathematics, Beck's monadicity theorem gives a criterion that characterises monadic functors, introduced by Jonathan Mock Beck in about 1964. It is often stated in dual form for comonads. It is sometimes called the Beck tripleability theorem because of the older term triple for a monad.

In category theory, an abstract branch of mathematics, distributive laws between monads are a way to express abstractly that two algebraic structures distribute one over the other.
Michael Barr is an American mathematician who is the Peter Redpath Emeritus Professor of Pure Mathematics at McGill University.
In the mathematical theory of categories, a sketch is a category D, together with a set of cones intended to be limits and a set of cocones intended to be colimits. A model of the sketch in a category C is a functor
In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.

Colin McLarty is an American logician whose publications have ranged widely in philosophy and the foundations of mathematics, as well as in the history of science and of mathematics.

Jacob Alexander Lurie is an American mathematician who is a professor at the Institute for Advanced Study. In 2014, Lurie received a MacArthur Fellowship.
James Edward Humphreys was an American mathematician who worked in algebraic groups, Lie groups, and Lie algebras and applications of these mathematical structures. He is known as the author of several mathematical texts, such as Introduction to Lie Algebras and Representation Theory and Reflection Groups and Coxeter Groups.
References
- ↑ Birth and Career Data from American Men and Women of Science, Thomson Gale 2004
- ↑ misterZ3r0 (26 June 2017). "Update on AbstractMath.org: a website that provided an introduction to advanced mathematics". reddit/learnmath. Archived from the original on 22 March 2018. Retrieved 2 November 2024.
I am sorry to inform the community that Professor Charles Wells who ran the website as a free resource passed away on June 17, 2017. I received a reply to an email inquiring Professor Wells why the website was down. Here was the reply: Hi Eugene... this Matt Wells, Charles' son. Sad to report that Dad died suddenly and peacefully on Saturday night. He left behind all of the instructions on how to fix the website, so we'll figure it out eventually. matt
{{cite news}}: CS1 maint: numeric names: authors list (link) - ↑ "Home page at CWRU". Archived from the original on 2016-12-31. Retrieved 2012-02-15.
- ↑ Negative review: Krantz, Steven G. (September 2004), "Book Review: A Handbook of Mathematical Discourse" (PDF), Notices of the American Mathematical Society, 51 (8): 897–898
- ↑ Positive review: Selden, Annie (February 27, 2014), "MAA Review: A Handbook of Mathematical Discourse", Mathematical Association of America Reviews
- ↑ Charles Wells, Chloe Maher, Oberlin Harmony (2002, Oberlin, Ohio). Incomplete table of contents given in: "Oberlin Harmony". Hymnary.org. Retrieved 18 January 2020.
- ↑ Pitts, A. (1991), "Review of Toposes, Triples and Theories by Barr, M., & Wells, C.", Journal of Symbolic Logic, 56 (1): 340–341, doi:10.2307/2274934, JSTOR 2274934
- ↑ Rota, Gian-Carlo (1986), "Toposes, Triples and Theories: M. Barr and C. Wells, Springer, 1985, 345 pp.", Advances in Mathematics , 61 (2): 184, doi: 10.1016/0001-8708(86)90076-9 ,
(complete review) The elements of category theory are presented with unsurpassed clarity and full motivation, and then applied to describe with equal cogency the closely related ideas of topoes, triples, and equationally defined algebraic theories. One or two more books like this one and universal algebra might take off.