Exact sequence

Illustration of an exact sequence of groups ${\displaystyle G_{i}}$ using Euler diagrams.

In mathematics, an exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next.

Definition

In the context of group theory, a sequence

${\displaystyle G_{0}\;{\xrightarrow {\ f_{1}\ }}\;G_{1}\;{\xrightarrow {\ f_{2}\ }}\;G_{2}\;{\xrightarrow {\ f_{3}\ }}\;\cdots \;{\xrightarrow {\ f_{n}\ }}\;G_{n}}$

of groups and group homomorphisms is said to be exactat${\displaystyle G_{i}}$ if ${\displaystyle \operatorname {im} (f_{i})=\ker(f_{i+1})}$. The sequence is called exact if it is exact at each ${\displaystyle G_{i}}$ for all ${\displaystyle 1\leq i<n}$, i.e., if the image of each homomorphism is equal to the kernel of the next.

The sequence of groups and homomorphisms may be either finite or infinite.

A similar definition can be made for other algebraic structures. For example, one could have an exact sequence of vector spaces and linear maps, or of modules and module homomorphisms. More generally, the notion of an exact sequence makes sense in any category with kernels and cokernels, and more specially in abelian categories, where it is widely used.

Simple cases

To understand the definition, it is helpful to consider relatively simple cases where the sequence is of group homomorphisms, is finite, and begins or ends with the trivial group. Traditionally, this, along with the single identity element, is denoted 0 (additive notation, usually when the groups are abelian), or denoted 1 (multiplicative notation).

• Consider the sequence 0 → A → B. The image of the leftmost map is 0. Therefore the sequence is exact if and only if the rightmost map (from A to B) has kernel {0}; that is, if and only if that map is a monomorphism (injective, or one-to-one).
• Consider the dual sequence B → C → 0. The kernel of the rightmost map is C. Therefore the sequence is exact if and only if the image of the leftmost map (from B to C) is all of C; that is, if and only if that map is an epimorphism (surjective, or onto).
• Therefore, the sequence 0 → X → Y → 0 is exact if and only if the map from X to Y is both a monomorphism and epimorphism (that is, a bimorphism), and so usually an isomorphism from X to Y (this always holds in exact categories like Set).

Short exact sequence

Short exact sequences are exact sequences of the form

${\displaystyle 0\to A\xrightarrow {f} B\xrightarrow {g} C\to 0.}$

As established above, for any such short exact sequence, f is a monomorphism and g is an epimorphism. Furthermore, the image of f is equal to the kernel of g. It is helpful to think of A as a subobject of B with f embedding A into B, and of C as the corresponding factor object (or quotient), B/A, with g inducing an isomorphism

${\displaystyle C\cong B/\operatorname {im} (f)=B/\operatorname {ker} (g)}$

The short exact sequence

${\displaystyle 0\to A\xrightarrow {f} B\xrightarrow {g} C\to 0\,}$

is called split if there exists a homomorphism h : C → B such that the composition g ∘ h is the identity map on C. It follows that if these are abelian groups, B is isomorphic to the direct sum of A and C:

${\displaystyle B\cong A\oplus C.}$

Long exact sequence

A general exact sequence is sometimes called a long exact sequence, to distinguish from the special case of a short exact sequence. ^[1]

A long exact sequence is equivalent to a family of short exact sequences in the following sense: Given a long sequence

${\displaystyle A_{0}\;\xrightarrow {\ f_{1}\ } \;A_{1}\;\xrightarrow {\ f_{2}\ } \;A_{2}\;\xrightarrow {\ f_{3}\ } \;\cdots \;\xrightarrow {\ f_{n}\ } \;A_{n},}$(1)

with n ≥ 2, we can split it up into the short sequences

${\displaystyle {\begin{aligned}0\rightarrow K_{1}\rightarrow {}&A_{1}\rightarrow K_{2}\rightarrow 0,\\0\rightarrow K_{2}\rightarrow {}&A_{2}\rightarrow K_{3}\rightarrow 0,\\&\ \,\vdots \\0\rightarrow K_{n-1}\rightarrow {}&A_{n-1}\rightarrow K_{n}\rightarrow 0,\\\end{aligned}}}$(2)

where ${\displaystyle K_{i}=\operatorname {im} (f_{i})}$ for every ${\displaystyle i}$. By construction, the sequences (2) are exact at the ${\displaystyle K_{i}}$'s (regardless of the exactness of (1)). Furthermore, (1) is a long exact sequence if and only if (2) are all short exact sequences.

See weaving lemma for details on how to re-form the long exact sequence from the short exact sequences.

Examples

Integers modulo two

Consider the following sequence of abelian groups:

${\displaystyle \mathbf {Z} \mathrel {\overset {2\times }{\,\hookrightarrow }} \mathbf {Z} \twoheadrightarrow \mathbf {Z} /2\mathbf {Z} }$

The first homomorphism maps each element i in the set of integers Z to the element 2i in Z. The second homomorphism maps each element i in Z to an element j in the quotient group; that is, j = i mod 2. Here the hook arrow ${\displaystyle \hookrightarrow }$ indicates that the map 2× from Z to Z is a monomorphism, and the two-headed arrow ${\displaystyle \twoheadrightarrow }$ indicates an epimorphism (the map mod 2). This is an exact sequence because the image 2Z of the monomorphism is the kernel of the epimorphism. Essentially "the same" sequence can also be written as

${\displaystyle 2\mathbf {Z} \mathrel {\,\hookrightarrow } \mathbf {Z} \twoheadrightarrow \mathbf {Z} /2\mathbf {Z} }$

In this case the monomorphism is 2n ↦ 2n and although it looks like an identity function, it is not onto (that is, not an epimorphism) because the odd numbers don't belong to 2Z. The image of 2Z through this monomorphism is however exactly the same subset of Z as the image of Z through n ↦ 2n used in the previous sequence. This latter sequence does differ in the concrete nature of its first object from the previous one as 2Z is not the same set as Z even though the two are isomorphic as groups.

The first sequence may also be written without using special symbols for monomorphism and epimorphism:

${\displaystyle 0\to \mathbf {Z} \mathrel {\overset {2\times }{\longrightarrow }} \mathbf {Z} \longrightarrow \mathbf {Z} /2\mathbf {Z} \to 0}$

Here 0 denotes the trivial group, the map from Z to Z is multiplication by 2, and the map from Z to the factor group Z/2Z is given by reducing integers modulo 2. This is indeed an exact sequence:

• the image of the map 0 → Z is {0}, and the kernel of multiplication by 2 is also {0}, so the sequence is exact at the first Z.
• the image of multiplication by 2 is 2Z, and the kernel of reducing modulo 2 is also 2Z, so the sequence is exact at the second Z.
• the image of reducing modulo 2 is Z/2Z, and the kernel of the zero map is also Z/2Z, so the sequence is exact at the position Z/2Z.

The first and third sequences are somewhat of a special case owing to the infinite nature of Z. It is not possible for a finite group to be mapped by inclusion (that is, by a monomorphism) as a proper subgroup of itself. Instead the sequence that emerges from the first isomorphism theorem is

${\displaystyle 1\to N\to G\to G/N\to 1}$

(here the trivial group is denoted ${\displaystyle 1,}$ as these groups are not supposed to be abelian).

As a more concrete example of an exact sequence on finite groups:

${\displaystyle 1\to C_{n}\to D_{2n}\to C_{2}\to 1}$

where ${\displaystyle C_{n}}$ is the cyclic group of order n and ${\displaystyle D_{2n}}$ is the dihedral group of order 2n, which is a non-abelian group.

Intersection and sum of modules

Let I and J be two ideals of a ring R. Then

${\displaystyle 0\to I\cap J\to I\oplus J\to I+J\to 0}$

is an exact sequence of R-modules, where the module homomorphism ${\displaystyle I\cap J\to I\oplus J}$ maps each element x of ${\displaystyle I\cap J}$ to the element ⁠${\displaystyle (x,x)}$⁠ of the direct sum ${\displaystyle I\oplus J}$, and the homomorphism ${\displaystyle I\oplus J\to I+J}$ maps each element ⁠${\displaystyle (x,y)}$⁠ of ${\displaystyle I\oplus J}$ to ⁠${\displaystyle x-y}$⁠.

These homomorphisms are restrictions of similarly defined homomorphisms that form the short exact sequence

${\displaystyle 0\to R\to R\oplus R\to R\to 0}$

Passing to quotient modules yields another exact sequence

${\displaystyle 0\to R/(I\cap J)\to R/I\oplus R/J\to R/(I+J)\to 0}$

Properties

The splitting lemma states that, for a short exact sequence

${\displaystyle 0\to A\;\xrightarrow {\ f\ } \;B\;\xrightarrow {\ g\ } \;C\to 0,}$ the following conditions are equivalent.

• There exists a morphism t : B → A such that t ∘ f is the identity on A.
• There exists a morphism u: C → B such that g ∘ u is the identity on C.
• There exists a morphism u: C → B such that B is the direct sum of f(A) and u(C).

For non-commutative groups, the splitting lemma does not apply, and one has only the equivalence between the two last conditions, with "the direct sum" replaced with "a semidirect product".

In both cases, one says that such a short exact sequence splits.

The snake lemma shows how a commutative diagram with two exact rows gives rise to a longer exact sequence. The nine lemma is a special case.

The five lemma gives conditions under which the middle map in a commutative diagram with exact rows of length 5 is an isomorphism; the short five lemma is a special case thereof applying to short exact sequences.

Weaving lemma

The importance of short exact sequences is underlined by the fact that every exact sequence results from "weaving together" several overlapping short exact sequences. Consider for instance the exact sequence

${\displaystyle A_{1}\to A_{2}\to A_{3}\to A_{4}\to A_{5}\to A_{6}}$

which implies that there exist objects C_k in the category such that

${\displaystyle C_{k}\cong \ker(A_{k}\to A_{k+1})\cong \operatorname {im} (A_{k-1}\to A_{k})}$.

Suppose in addition that the cokernel of each morphism exists, and is isomorphic to the image of the next morphism in the sequence:

${\displaystyle C_{k}\cong \operatorname {coker} (A_{k-2}\to A_{k-1})}$

(This is true for a number of interesting categories, including any abelian category such as the abelian groups; but it is not true for all categories that allow exact sequences, and in particular is not true for the category of groups, in which coker(f) : G → H is not H/im(f) but ${\displaystyle H/{\left\langle \operatorname {im} f\right\rangle }^{H}}$, the quotient of H by the conjugate closure of im(f).) Then we obtain a commutative diagram in which all the diagonals are short exact sequences:

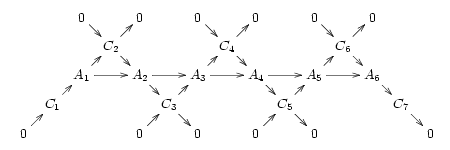
The only portion of this diagram that depends on the cokernel condition is the object ${\textstyle C_{7}}$ and the final pair of morphisms ${\textstyle A_{6}\to C_{7}\to 0}$. If there exists any object ${\displaystyle A_{k+1}}$ and morphism ${\displaystyle A_{k}\to A_{k+1}}$ such that ${\displaystyle A_{k-1}\to A_{k}\to A_{k+1}}$ is exact, then the exactness of ${\displaystyle 0\to C_{k}\to A_{k}\to C_{k+1}\to 0}$ is ensured. Again taking the example of the category of groups, the fact that im(f) is the kernel of some homomorphism on H implies that it is a normal subgroup, which coincides with its conjugate closure; thus coker(f) is isomorphic to the image H/im(f) of the next morphism.

Conversely, given any list of overlapping short exact sequences, their middle terms form an exact sequence in the same manner.

Applications of exact sequences

In the theory of abelian categories, short exact sequences are often used as a convenient language to talk about subobjects and factor objects.

The extension problem is essentially the question "Given the end terms A and C of a short exact sequence, what possibilities exist for the middle term B?" In the category of groups, this is equivalent to the question, what groups B have A as a normal subgroup and C as the corresponding factor group? This problem is important in the classification of groups. See also Outer automorphism group.

Notice that in an exact sequence, the composition f_i+1 ∘ f_i maps A_i to 0 in A_i+2, so every exact sequence is a chain complex. Furthermore, only f_i-images of elements of A_i are mapped to 0 by f_i+1, so the homology of this chain complex is trivial. More succinctly:

Exact sequences are precisely those chain complexes which are acyclic.

Given any chain complex, its homology can therefore be thought of as a measure of the degree to which it fails to be exact.

If we take a series of short exact sequences linked by chain complexes (that is, a short exact sequence of chain complexes, or from another point of view, a chain complex of short exact sequences), then we can derive from this a long exact sequence (that is, an exact sequence indexed by the natural numbers) on homology by application of the zig-zag lemma. It comes up in algebraic topology in the study of relative homology; the Mayer–Vietoris sequence is another example. Long exact sequences induced by short exact sequences are also characteristic of derived functors.

Exact functors are functors that transform exact sequences into exact sequences.

References

Citations

1. "exact sequence in nLab, Remark 2.3". ncatlab.org. Retrieved 2021-09-05.

Sources

• Spanier, Edwin Henry (1995). Algebraic Topology . Berlin: Springer. p.  179. ISBN   0-387-94426-5.
• Eisenbud, David (1995). Commutative Algebra: with a View Toward Algebraic Geometry . Springer-Verlag New York. p.  785. ISBN   0-387-94269-6.