In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
Geometric topology as an area distinct from algebraic topology may be said to have originated in the 1935 classification of lens spaces by Reidemeister torsion, which required distinguishing spaces that are homotopy equivalent but not homeomorphic. This was the origin of simple homotopy theory. The use of the term geometric topology to describe these seems to have originated rather recently. [1]
Manifolds differ radically in behavior in high and low dimension.
High-dimensional topology refers to manifolds of dimension 5 and above, or in relative terms, embeddings in codimension 3 and above. Low-dimensional topology is concerned with questions in dimensions up to 4, or embeddings in codimension up to 2.
Dimension 4 is special, in that in some respects (topologically), dimension 4 is high-dimensional, while in other respects (differentiably), dimension 4 is low-dimensional; this overlap yields phenomena exceptional to dimension 4, such as exotic differentiable structures on R4. Thus the topological classification of 4-manifolds is in principle tractable, and the key questions are: does a topological manifold admit a differentiable structure, and if so, how many? Notably, the smooth case of dimension 4 is the last open case of the generalized Poincaré conjecture; see Gluck twists.
The distinction is because surgery theory works in dimension 5 and above (in fact, in many cases, it works topologically in dimension 4, though this is very involved to prove), and thus the behavior of manifolds in dimension 5 and above may be studied using the surgery theory program. In dimension 4 and below (topologically, in dimension 3 and below), surgery theory does not work. Indeed, one approach to discussing low-dimensional manifolds is to ask "what would surgery theory predict to be true, were it to work?" – and then understand low-dimensional phenomena as deviations from this.
The precise reason for the difference at dimension 5 is because the Whitney embedding theorem, the key technical trick which underlies surgery theory, requires 2+1 dimensions. Roughly, the Whitney trick allows one to "unknot" knotted spheres – more precisely, remove self-intersections of immersions; it does this via a homotopy of a disk – the disk has 2 dimensions, and the homotopy adds 1 more – and thus in codimension greater than 2, this can be done without intersecting itself; hence embeddings in codimension greater than 2 can be understood by surgery. In surgery theory, the key step is in the middle dimension, and thus when the middle dimension has codimension more than 2 (loosely, 2½ is enough, hence total dimension 5 is enough), the Whitney trick works. The key consequence of this is Smale's h-cobordism theorem, which works in dimension 5 and above, and forms the basis for surgery theory.
A modification of the Whitney trick can work in 4 dimensions, and is called Casson handles – because there are not enough dimensions, a Whitney disk introduces new kinks, which can be resolved by another Whitney disk, leading to a sequence ("tower") of disks. The limit of this tower yields a topological but not differentiable map, hence surgery works topologically but not differentiably in dimension 4.
In all dimensions, the fundamental group of a manifold is a very important invariant, and determines much of the structure; in dimensions 1, 2 and 3, the possible fundamental groups are restricted, while in dimension 4 and above every finitely presented group is the fundamental group of a manifold (note that it is sufficient to show this for 4- and 5-dimensional manifolds, and then to take products with spheres to get higher ones).
A manifold is orientable if it has a consistent choice of orientation, and a connected orientable manifold has exactly two different possible orientations. In this setting, various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods of homology theory, whereas for differentiable manifolds more structure is present, allowing a formulation in terms of differential forms. An important generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (a fiber bundle) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.
A handle decomposition of an m-manifold M is a union
where each is obtained from by the attaching of -handles. A handle decomposition is to a manifold what a CW-decomposition is to a topological space—in many regards the purpose of a handle decomposition is to have a language analogous to CW-complexes, but adapted to the world of smooth manifolds. Thus an i-handle is the smooth analogue of an i-cell. Handle decompositions of manifolds arise naturally via Morse theory. The modification of handle structures is closely linked to Cerf theory.
Local flatness is a property of a submanifold in a topological manifold of larger dimension. In the category of topological manifolds, locally flat submanifolds play a role similar to that of embedded submanifolds in the category of smooth manifolds.
Suppose a d dimensional manifold N is embedded into an n dimensional manifold M (where d<n). If we say N is locally flat at x if there is a neighborhood of x such that the topological pair is homeomorphic to the pair , with a standard inclusion of as a subspace of . That is, there exists a homeomorphism such that the image of coincides with .
The generalized Schoenflies theorem states that, if an (n − 1)-dimensional sphere S is embedded into the n-dimensional sphere Sn in a locally flat way (that is, the embedding extends to that of a thickened sphere), then the pair (Sn, S) is homeomorphic to the pair (Sn, Sn−1), where Sn−1 is the equator of the n-sphere. Brown and Mazur received the Veblen Prize for their independent proofs [2] [3] of this theorem.
Low-dimensional topology includes:
each have their own theory, where there are some connections.
Low-dimensional topology is strongly geometric, as reflected in the uniformization theorem in 2 dimensions – every surface admits a constant curvature metric; geometrically, it has one of 3 possible geometries: positive curvature/spherical, zero curvature/flat, negative curvature/hyperbolic – and the geometrization conjecture (now theorem) in 3 dimensions – every 3-manifold can be cut into pieces, each of which has one of 8 possible geometries.
2-dimensional topology can be studied as complex geometry in one variable (Riemann surfaces are complex curves) – by the uniformization theorem every conformal class of metrics is equivalent to a unique complex one, and 4-dimensional topology can be studied from the point of view of complex geometry in two variables (complex surfaces), though not every 4-manifold admits a complex structure.
Knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3 (since we're using topology, a circle isn't bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
To gain further insight, mathematicians have generalized the knot concept in several ways. Knots can be considered in other three-dimensional spaces and objects other than circles can be used; see knot (mathematics) . Higher-dimensional knots are n-dimensional spheres in m-dimensional Euclidean space.
In high-dimensional topology, characteristic classes are a basic invariant, and surgery theory is a key theory.
A characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not. In other words, characteristic classes are global invariants which measure the deviation of a local product structure from a global product structure. They are one of the unifying geometric concepts in algebraic topology, differential geometry and algebraic geometry.
Surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by Milnor ( 1961 ). Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along the cut or boundary. This is closely related to, but not identical with, handlebody decompositions. It is a major tool in the study and classification of manifolds of dimension greater than 3.
More technically, the idea is to start with a well-understood manifold M and perform surgery on it to produce a manifold M ′ having some desired property, in such a way that the effects on the homology, homotopy groups, or other interesting invariants of the manifold are known.
The classification of exotic spheres by Kervaire and Milnor ( 1963 ) led to the emergence of surgery theory as a major tool in high-dimensional topology.
In mathematics, differential topology is the field dealing with the topological properties and smooth properties of smooth manifolds. In this sense differential topology is distinct from the closely related field of differential geometry, which concerns the geometric properties of smooth manifolds, including notions of size, distance, and rigid shape. By comparison differential topology is concerned with coarser properties, such as the number of holes in a manifold, its homotopy type, or the structure of its diffeomorphism group. Because many of these coarser properties may be captured algebraically, differential topology has strong links to algebraic topology.
Topology is the branch of mathematics concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.
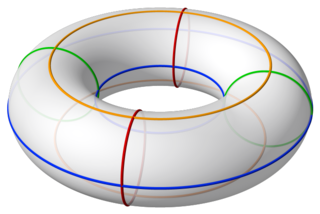
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory.
In mathematics, and specifically in topology, a CW complex is a topological space that is built by gluing together topological balls of different dimensions in specific ways. It generalizes both manifolds and simplicial complexes and has particular significance for algebraic topology. It was initially introduced by J. H. C. Whitehead to meet the needs of homotopy theory. CW complexes have better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation.
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds of the same dimension are cobordant if their disjoint union is the boundary of a compact manifold one dimension higher.
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, to submanifolds in manifolds, and suitable subsets of algebraic varieties.
In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds. Handles are used to particularly study 3-manifolds.
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, more precisely in topology and differential geometry, a hyperbolic 3-manifold is a manifold of dimension 3 equipped with a hyperbolic metric, that is a Riemannian metric which has all its sectional curvatures equal to −1. It is generally required that this metric be also complete: in this case the manifold can be realised as a quotient of the 3-dimensional hyperbolic space by a discrete group of isometries.
In mathematics, a 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure, and even if there exists a smooth structure, it need not be unique.
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.
In mathematics, an exotic is a differentiable manifold that is homeomorphic but not diffeomorphic to the Euclidean space The first examples were found in 1982 by Michael Freedman and others, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's theorems about smooth 4-manifolds. There is a continuum of non-diffeomorphic differentiable structures as was shown first by Clifford Taubes.
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of manifolds to infinite-dimensional setting. Analogous to the finite-dimensional situation, one can define a differentiable Hilbert manifold by considering a maximal atlas in which the transition maps are differentiable.
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one finite-dimensional manifold from another in a 'controlled' way, introduced by John Milnor. Milnor called this technique surgery, while Andrew Wallace called it spherical modification. The "surgery" on a differentiable manifold M of dimension , could be described as removing an imbedded sphere of dimension p from M. Originally developed for differentiable manifolds, surgery techniques also apply to piecewise linear (PL-) and topological manifolds.
In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential pushforward is everywhere injective. Explicitly, f : M → N is an immersion if
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain.
In differential topology, a branch of mathematics, a stratifold is a generalization of a differentiable manifold where certain kinds of singularities are allowed. More specifically a stratifold is stratified into differentiable manifolds of (possibly) different dimensions. Stratifolds can be used to construct new homology theories. For example, they provide a new geometric model for ordinary homology. The concept of stratifolds was invented by Matthias Kreck. The basic idea is similar to that of a topologically stratified space, but adapted to differential topology.
| Fields |  | |
|---|---|---|
| Key concepts | ||
| Metrics and properties | ||
| Key results | ||
