In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C that makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.
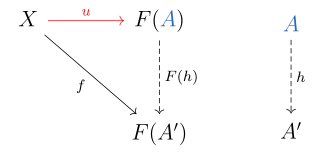
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Informally, the notion of a natural transformation states that a particular map between functors can be done consistently over an entire category.

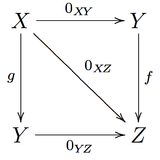
In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, a branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X.
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.

Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert.
In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.
In mathematics, a sheaf is a tool for systematically tracking data attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set.
In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products within a given category.
In mathematics, a triangulated category is a category with the additional structure of a "translation functor" and a class of "exact triangles". Prominent examples are the derived category of an abelian category, as well as the stable homotopy category. The exact triangles generalize the short exact sequences in an abelian category, as well as fiber sequences and cofiber sequences in topology.
In category theory, a branch of mathematics, a subfunctor is a special type of functor that is an analogue of a subset.
This is a glossary of properties and concepts in category theory in mathematics.
In mathematics, a quotient category is a category obtained from another category by identifying sets of morphisms. Formally, it is a quotient object in the category of categories, analogous to a quotient group or quotient space, but in the categorical setting.
In mathematics, a morphism is a concept of category theory that generalizes structure-preserving maps such as homomorphism between algebraic structures, functions from a set to another set, and continuous functions between topological spaces. Although many examples of morphisms are structure-preserving maps, morphisms need not to be maps, but they can be composed in a way that is similar to function composition.