Elaboration and example
Given a function

with domain  , the range of
, the range of  , sometimes denoted
, sometimes denoted  or
or  , [4] may refer to the codomain or target set
, [4] may refer to the codomain or target set  (i.e., the set into which all of the output of
(i.e., the set into which all of the output of  is constrained to fall), or to
is constrained to fall), or to  , the image of the domain of
, the image of the domain of  under
under  (i.e., the subset of
(i.e., the subset of  consisting of all actual outputs of
consisting of all actual outputs of  ). The image of a function is always a subset of the codomain of the function. [5]
). The image of a function is always a subset of the codomain of the function. [5]
As an example of the two different usages, consider the function  as it is used in real analysis (that is, as a function that inputs a real number and outputs its square). In this case, its codomain is the set of real numbers
as it is used in real analysis (that is, as a function that inputs a real number and outputs its square). In this case, its codomain is the set of real numbers  , but its image is the set of non-negative real numbers
, but its image is the set of non-negative real numbers  , since
, since  is never negative if
is never negative if  is real. For this function, if we use "range" to mean codomain, it refers to
is real. For this function, if we use "range" to mean codomain, it refers to  ; if we use "range" to mean image, it refers to
; if we use "range" to mean image, it refers to  .
.
For some functions, the image and the codomain coincide; these functions are called surjective or onto. For example, consider the function  which inputs a real number and outputs its double. For this function, both the codomain and the image are the set of all real numbers, so the word range is unambiguous.
which inputs a real number and outputs its double. For this function, both the codomain and the image are the set of all real numbers, so the word range is unambiguous.
Even in cases where the image and codomain of a function are different, a new function can be uniquely defined with its codomain as the image of the original function. For example, as a function from the integers to the integers, the doubling function  is not surjective because only the even integers are part of the image. However, a new function
is not surjective because only the even integers are part of the image. However, a new function  whose domain is the integers and whose codomain is the even integers is surjective. For
whose domain is the integers and whose codomain is the even integers is surjective. For  the word range is unambiguous.
the word range is unambiguous.
In mathematics, a binary relation associates elements of one set called the domain with elements of another set called the codomain. Precisely, a binary relation over sets and is a set of ordered pairs where is in and is in . It encodes the common concept of relation: an element is related to an element , if and only if the pair belongs to the set of ordered pairs that defines the binary relation.

A bijection, bijective function, or one-to-one correspondence between two mathematical sets is a function such that each element of the second set is the image of exactly one element of the first set. Equivalently, a bijection is a relation between two sets such that each element of either set is paired with exactly one element of the other set.

In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that
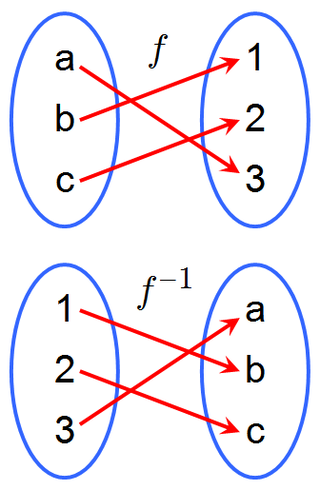
In mathematics, the inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by
In mathematics, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain, every nonzero element a has the cancellation property, that is, if a ≠ 0, an equality ab = ac implies b = c.
In mathematics, a partial functionf from a set X to a set Y is a function from a subset S of X to Y. The subset S, that is, the domain of f viewed as a function, is called the domain of definition or natural domain of f. If S equals X, that is, if f is defined on every element in X, then f is said to be a total function.
In mathematics, and more specifically in ring theory, an ideal of a ring is a special subset of its elements. Ideals generalize certain subsets of the integers, such as the even numbers or the multiples of 3. Addition and subtraction of even numbers preserves evenness, and multiplying an even number by any integer results in an even number; these closure and absorption properties are the defining properties of an ideal. An ideal can be used to construct a quotient ring in a way similar to how, in group theory, a normal subgroup can be used to construct a quotient group.
In mathematics, a surjective function (also known as surjection, or onto function ) is a function f such that, for every element y of the function's codomain, there exists at least one element x in the function's domain such that f(x) = y. In other words, for a function f : X → Y, the codomain Y is the image of the function's domain X. It is not required that x be unique; the function f may map one or more elements of X to the same element of Y.
In mathematics, weak topology is an alternative term for certain initial topologies, often on topological vector spaces or spaces of linear operators, for instance on a Hilbert space. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual. The remainder of this article will deal with this case, which is one of the concepts of functional analysis.
In mathematics, an injective function (also known as injection, or one-to-one function ) is a function f that maps distinct elements of its domain to distinct elements of its codomain; that is, x1 ≠ x2 implies f(x1) ≠ f(x2) (equivalently by contraposition, f(x1) = f(x2) implies x1 = x2). In other words, every element of the function's codomain is the image of at most one element of its domain. The term one-to-one function must not be confused with one-to-one correspondence that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain.
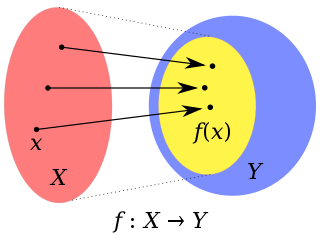
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by or , where f is the function. In layman's terms, the domain of a function can generally be thought of as "what x can be".

In mathematics, a codomain or set of destination of a function is a set into which all of the output of the function is constrained to fall. It is the set Y in the notation f: X → Y. The term range is sometimes ambiguously used to refer to either the codomain or the image of a function.

In abstract algebra, a generating set of a group is a subset of the group set such that every element of the group can be expressed as a combination of finitely many elements of the subset and their inverses.
In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
In mathematics, the Gelfand representation in functional analysis is either of two things:
In mathematics, more specifically in topology, an open map is a function between two topological spaces that maps open sets to open sets. That is, a function is open if for any open set in the image is open in Likewise, a closed map is a function that maps closed sets to closed sets. A map may be open, closed, both, or neither; in particular, an open map need not be closed and vice versa.
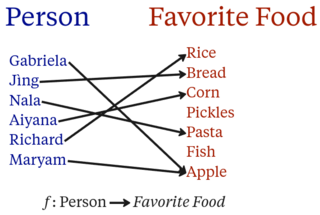
In mathematics, for a function , the image of an input value is the single output value produced by when passed . The preimage of an output value is the set of input values that produce .
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers , or a subset of that contains an interval of positive length. Most real functions that are considered and studied are differentiable in some interval. The most widely considered such functions are the real functions, which are the real-valued functions of a real variable, that is, the functions of a real variable whose codomain is the set of real numbers.

In mathematics, injections, surjections, and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.



























