In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
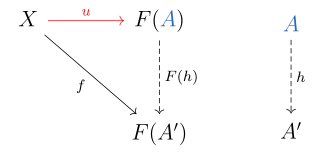
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In mathematics, the Yoneda lemma is a fundamental result in category theory. It is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory. It allows the embedding of any locally small category into a category of functors defined on that category. It also clarifies how the embedded category, of representable functors and their natural transformations, relates to the other objects in the larger functor category. It is an important tool that underlies several modern developments in algebraic geometry and representation theory. It is named after Nobuo Yoneda.
In commutative algebra, the prime spectrum of a commutative ring R is the set of all prime ideals of R, and is usually denoted by ; in algebraic geometry it is simultaneously a topological space equipped with the sheaf of rings .
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In mathematics, a sheaf is a tool for systematically tracking data attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set.
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set A can be thought of as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices.
In category theory, a branch of mathematics, a monad is a monoid in the category of endofunctors of some fixed category. An endofunctor is a functor mapping a category to itself, and a monad is an endofunctor together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories. Monads are also useful in the theory of datatypes, the denotational semantics of imperative programming languages, and in functional programming languages, allowing languages without mutable state to do things such as simulate for-loops; see Monad.
In category theory, a branch of mathematics, a functor category is a category where the objects are the functors and the morphisms are natural transformations between the functors. Functor categories are of interest for two main reasons:
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
In mathematics, especially in category theory, a closed monoidal category is a category that is both a monoidal category and a closed category in such a way that the structures are compatible.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, the notion of a projective object generalizes the notion of a projective module. Projective objects in abelian categories are used in homological algebra. The dual notion of a projective object is that of an injective object.
In mathematics, the direct image functor is a construction in sheaf theory that generalizes the global sections functor to the relative case. It is of fundamental importance in topology and algebraic geometry. Given a sheaf F defined on a topological space X and a continuous map f: X → Y, we can define a new sheaf f∗F on Y, called the direct image sheaf or the pushforward sheaf of F along f, such that the global sections of f∗F is given by the global sections of F. This assignment gives rise to a functor f∗ from the category of sheaves on X to the category of sheaves on Y, which is known as the direct image functor. Similar constructions exist in many other algebraic and geometric contexts, including that of quasi-coherent sheaves and étale sheaves on a scheme.
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a morphism that preserve monoidal multiplication and unit, respectively. Mathematicians require these coherence maps to satisfy additional properties depending on how strictly they want to preserve the monoidal structure; each of these properties gives rise to a slightly different definition of monoidal functors
In mathematics, a Grothendieck category is a certain kind of abelian category, introduced in Alexander Grothendieck's Tôhoku paper of 1957 in order to develop the machinery of homological algebra for modules and for sheaves in a unified manner. The theory of these categories was further developed in Pierre Gabriel's seminal thesis in 1962.
In mathematics, a sheaf of O-modules or simply an O-module over a ringed space (X, O) is a sheaf F such that, for any open subset U of X, F(U) is an O(U)-module and the restriction maps F(U) → F(V) are compatible with the restriction maps O(U) → O(V): the restriction of fs is the restriction of f times the restriction of s for any f in O(U) and s in F(U).























