In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.

In logic, mathematics and linguistics, and is the truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as or or (prefix) or or in which is the most modern and widely used.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning.
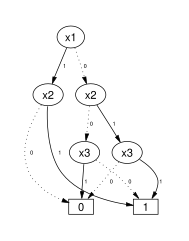
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.
An influence diagram (ID) is a compact graphical and mathematical representation of a decision situation. It is a generalization of a Bayesian network, in which not only probabilistic inference problems but also decision making problems can be modeled and solved.

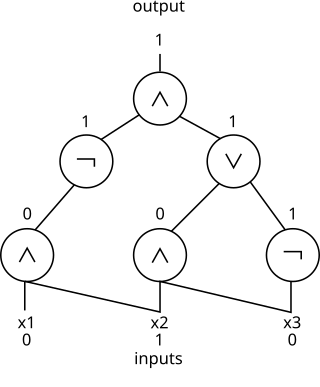
An and-inverter graph (AIG) is a directed, acyclic graph that represents a structural implementation of the logical functionality of a circuit or network. An AIG consists of two-input nodes representing logical conjunction, terminal nodes labeled with variable names, and edges optionally containing markers indicating logical negation. This representation of a logic function is rarely structurally efficient for large circuits, but is an efficient representation for manipulation of boolean functions. Typically, the abstract graph is represented as a data structure in software.
Probabilistic logic involves the use of probability and logic to deal with uncertain situations. Probabilistic logic extends traditional logic truth tables with probabilistic expressions. A difficulty of probabilistic logics is their tendency to expand the computational complexities of their probabilistic and logical components. Other difficulties include the possibility of counter-intuitive results, such as in case of belief fusion in Dempster–Shafer theory. Source trust and epistemic uncertainty about the probabilities they provide, such as defined in subjective logic, are additional elements to consider. The need to deal with a broad variety of contexts and issues has led to many different proposals.
In logic, a functionally complete set of logical connectives or Boolean operators is one that can be used to express all possible truth tables by combining members of the set into a Boolean expression. A well-known complete set of connectives is { AND, NOT }. Each of the singleton sets { NAND } and { NOR } is functionally complete. However, the set { AND, OR } is incomplete, due to its inability to express NOT.
In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible input length.
In database theory, a conjunctive query is a restricted form of first-order queries using the logical conjunction operator. Many first-order queries can be written as conjunctive queries. In particular, a large part of queries issued on relational databases can be expressed in this way. Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries do not share.
In model theory, interpretation of a structure M in another structure N is a technical notion that approximates the idea of representing M inside N. For example, every reduct or definitional expansion of a structure N has an interpretation in N.
Symbolic circuit analysis is a formal technique of circuit analysis to calculate the behaviour or characteristic of an electric/electronic circuit with the independent variables, the dependent variables, and the circuit elements represented by symbols.
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematical model for digital logic circuits. Circuits are defined by the gates they contain and the values the gates can produce. For example, the values in a Boolean circuit are Boolean values, and the circuit includes conjunction, disjunction, and negation gates. The values in an integer circuit are sets of integers and the gates compute set union, set intersection, and set complement, as well as the arithmetic operations addition and multiplication.
The Tseytin transformation, alternatively written Tseitin transformation, takes as input an arbitrary combinatorial logic circuit and produces an equisatisfiable boolean formula in conjunctive normal form (CNF). The length of the formula is linear in the size of the circuit. Input vectors that make the circuit output "true" are in 1-to-1 correspondence with assignments that satisfy the formula. This reduces the problem of circuit satisfiability on any circuit to the satisfiability problem on 3-CNF formulas. It was discovered by the Russian scientist Grigori Tseitin.
A graphoid is a set of statements of the form, "X is irrelevant to Y given that we know Z" where X, Y and Z are sets of variables. The notion of "irrelevance" and "given that we know" may obtain different interpretations, including probabilistic, relational and correlational, depending on the application. These interpretations share common properties that can be captured by paths in graphs. The theory of graphoids characterizes these properties in a finite set of axioms that are common to informational irrelevance and its graphical representations.
In the mathematical field of graph theory, an agreement forest for two given trees is any forest which can, informally speaking, be obtained from both trees by removing a common number of edges.
An algebraic decision diagram (ADD) or a multi-terminal binary decision diagram (MTBDD), is a data structure that is used to symbolically represent a Boolean function whose codomain is an arbitrary finite set S. An ADD is an extension of a reduced ordered binary decision diagram, or commonly named binary decision diagram (BDD) in the literature, which terminal nodes are not restricted to the Boolean values 0 (FALSE) and 1 (TRUE). The terminal nodes may take any value from a set of constants S.