Related Research Articles
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
In mathematical logic, a formula is in negation normal form (NNF) if the negation operator (, not) is only applied to variables and the only other allowed Boolean operators are conjunction (, and) and disjunction (, or).
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression.

In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
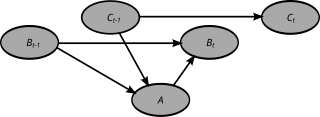
A dynamic Bayesian network (DBN) is a Bayesian network (BN) which relates variables to each other over adjacent time steps.
Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics and to a lesser extent computer science. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
Logic optimization is a process of finding an equivalent representation of the specified logic circuit under one or more specified constraints. This process is a part of a logic synthesis applied in digital electronics and integrated circuit design.

Diagrammatic reasoning is reasoning by means of visual representations. The study of diagrammatic reasoning is about the understanding of concepts and ideas, visualized with the use of diagrams and imagery instead of by linguistic or algebraic means.
Knowledge compilation is a family of approaches for addressing the intractability of a number of artificial intelligence problems.
In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified, using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false. If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT.
The constraint composite graph is a node-weighted undirected graph associated with a given combinatorial optimization problem posed as a weighted constraint satisfaction problem. Developed and introduced by Satish Kumar Thittamaranahalli, the idea of the constraint composite graph is a big step towards unifying different approaches for exploiting "structure" in weighted constraint satisfaction problems.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.
In computer science, the Sharp Satisfiability Problem is the problem of counting the number of interpretations that satisfy a given Boolean formula, introduced by Valiant in 1979. In other words, it asks in how many ways the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. For example, the formula is satisfiable by three distinct boolean value assignments of the variables, namely, for any of the assignments, , and, we have
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations in the same way that elementary algebra describes numerical operations.
In theoretical computer science, monotone dualization is a computational problem of constructing the dual of a monotone Boolean function. Equivalent problems can also be formulated as constructing the transversal hypergraph of a given hypergraph, of listing all minimal hitting sets of a family of sets, or of listing all minimal set covers of a family of sets. These problems can be solved in quasi-polynomial time in the combined size of its input and output, but whether they can be solved in polynomial time is an open problem.
Probabilistic logic programming is a programming paradigm that combines logic programming with probabilities.
References
- ↑ Darwiche, Adnan; Marquis, Pierre; Suciu, Dan; Szeider, Stefan (2018). Recent trends in knowledge compilation (Report). Schloss Dagstuhl.
- 1 2 3 Darwiche, Adnan (2011). "SDD: A New Canonical Representation of Propositional Knowledge Bases". International Joint Conference on Artificial Intelligence.
- 1 2 Riguzzi, Fabrizio (2023). Foundations of probabilistic logic programming: Languages, semantics, inference and learning (2nd ed.). Gistrup, Denmark: River Publishers. p. 214. ISBN 978-87-7022-719-3.
- ↑ Vlasselaer, J., Renkens, J., Van den Broeck, G., & De Raedt, L. (2014). Compiling probabilistic logic programs into sentential decision diagrams. In Proceedings Workshop on Probabilistic Logic Programming (PLP) (pp. 1-10).
- ↑ Bova, Simone (2016). SDDs are exponentially more succinct than OBDDs. AAAI Conference on Artificial Intelligence.
- ↑ Kisa, Doga; Van den Broeck, Guy; Choi, Arthur; Darwiche, Adnan (2014). Probabilistic Sentential Decision Diagrams. International Conference on the Principles of Knowledge Representation and Reasoning (KR).