Prolog is a logic programming language that has its origins in artificial intelligence and computational linguistics.
Inductive logic programming (ILP) is a subfield of symbolic artificial intelligence which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. The term "inductive" here refers to philosophical rather than mathematical induction. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.
In theoretical computer science, a probabilistic Turing machine is a non-deterministic Turing machine that chooses between the available transitions at each point according to some probability distribution. As a consequence, a probabilistic Turing machine can—unlike a deterministic Turing Machine—have stochastic results; that is, on a given input and instruction state machine, it may have different run times, or it may not halt at all; furthermore, it may accept an input in one execution and reject the same input in another execution.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
Grammar theory to model symbol strings originated from work in computational linguistics aiming to understand the structure of natural languages. Probabilistic context free grammars (PCFGs) have been applied in probabilistic modeling of RNA structures almost 40 years after they were introduced in computational linguistics.
Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word infer means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in Europe dates at least to Aristotle. Deduction is inference deriving logical conclusions from premises known or assumed to be true, with the laws of valid inference being studied in logic. Induction is inference from particular evidence to a universal conclusion. A third type of inference is sometimes distinguished, notably by Charles Sanders Peirce, contradistinguishing abduction from induction.
In the field of information retrieval, divergence from randomness, one of the first models, is one type of probabilistic model. It is basically used to test the amount of information carried in the documents. It is based on Harter's 2-Poisson indexing-model. The 2-Poisson model has a hypothesis that the level of the documents is related to a set of documents which contains words occur relatively greater than the rest of the documents. It is not a 'model', but a framework for weighting terms using probabilistic methods, and it has a special relationship for term weighting based on notion of eliteness.
Answer set programming (ASP) is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers—programs for generating stable models—are used to perform search. The computational process employed in the design of many answer set solvers is an enhancement of the DPLL algorithm and, in principle, it always terminates.
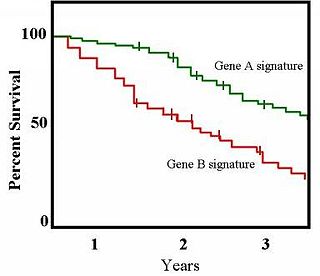
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the Journal of the American Statistical Association. The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited more than 61,800 times since its publication in 1958.
A Markov logic network (MLN) is a probabilistic logic which applies the ideas of a Markov network to first-order logic, defining probability distributions on possible worlds on any given domain.
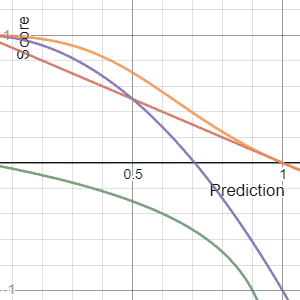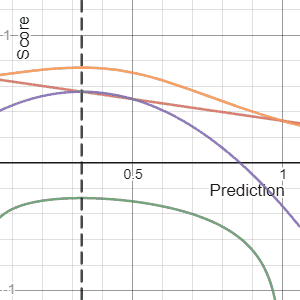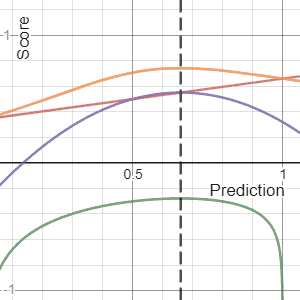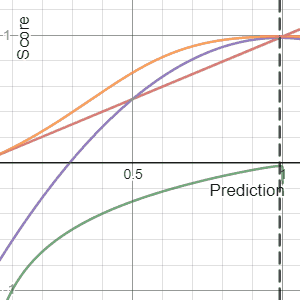
In decision theory, a scoring rule provides a summary measure for the evaluation of probabilistic predictions or forecasts. It is applicable to tasks in which predictions assign probabilities to events, i.e. one issues a probability distribution as prediction. This includes probabilistic classification of a set of mutually exclusive outcomes or classes.
The concept of a stable model, or answer set, is used to define a declarative semantics for logic programs with negation as failure. This is one of several standard approaches to the meaning of negation in logic programming, along with program completion and the well-founded semantics. The stable model semantics is the basis of answer set programming.
The Binary Independence Model (BIM) in computing and information science is a probabilistic information retrieval technique. The model makes some simple assumptions to make the estimation of document/query similarity probable and feasible.
The query likelihood model is a language model used in information retrieval. A language model is constructed for each document in the collection. It is then possible to rank each document by the probability of specific documents given a query. This is interpreted as being the likelihood of a document being relevant given a query.
Probabilistic programming (PP) is a programming paradigm in which probabilistic models are specified and inference for these models is performed automatically. It represents an attempt to unify probabilistic modeling and traditional general purpose programming in order to make the former easier and more widely applicable. It can be used to create systems that help make decisions in the face of uncertainty.

Bayesian programming is a formalism and a methodology for having a technique to specify probabilistic models and solve problems when less than the necessary information is available.

ProbOnto is a knowledge base and ontology of probability distributions. ProbOnto 2.5 contains over 150 uni- and multivariate distributions and alternative parameterizations, more than 220 relationships and re-parameterization formulas, supporting also the encoding of empirical and univariate mixture distributions.
Logic programming is a programming paradigm that includes languages based on formal logic, including Datalog and Prolog. This article describes the syntax and semantics of the purely declarative subset of these languages. Confusingly, the name "logic programming" also refers to a specific programming language that roughly corresponds to the declarative subset of Prolog. Unfortunately, the term must be used in both senses in this article.
Probabilistic logic programming is a programming paradigm that combines logic programming with probabilities.
In artificial intelligence, a sentential decision diagram (SDD) is a type of knowledge representation used in knowledge compilation to represent Boolean functions. SDDs can be viewed as a generalization of the influential ordered binary decision diagram (OBDD) representation, by allowing decisions on multiple variables at once. Like OBDDs, SDDs allow for tractable Boolean operations, while being exponentially more succinct. For this reason, they have become an important representation in knowledge compilation.

















