In mathematics, a read-once function is a special type of Boolean function that can be described by a Boolean expression in which each variable appears only once.
More precisely, the expression is required to use only the operations of logical conjunction, logical disjunction, and negation. By applying De Morgan's laws, such an expression can be transformed into one in which negation is used only on individual variables (still with each variable appearing only once). By replacing each negated variable with a new positive variable representing its negation, such a function can be transformed into an equivalent positive read-once Boolean function, represented by a read-once expression without negations. [1]
For example, for three variables a, b, and c, the expressions
are all read-once (as are the other functions obtained by permuting the variables in these expressions). However, the Boolean median operation, given by the expression
is not read-once: this formula has more than one copy of each variable, and there is no equivalent formula that uses each variable only once. [2]
The disjunctive normal form of a (positive) read-once function is not generally itself read-once. Nevertheless, it carries important information about the function. In particular, if one forms a co-occurrence graph in which the vertices represent variables, and edges connect pairs of variables that both occur in the same clause of the conjunctive normal form, then the co-occurrence graph of a read-once function is necessarily a cograph. More precisely, a positive Boolean function is read-once if and only if its co-occurrence graph is a cograph, and in addition every maximal clique of the co-occurrence graph forms one of the conjunctions (prime implicants) of the disjunctive normal form. [3] That is, when interpreted as a function on sets of vertices of its co-occurrence graph, a read-once function is true for sets of vertices that contain a maximal clique, and false otherwise. For instance the median function has the same co-occurrence graph as the conjunction of three variables, a triangle graph, but the three-vertex complete subgraph of this graph (the whole graph) forms a subset of a clause only for the conjunction and not for the median. [4] Two variables of a positive read-once expression are adjacent in the co-occurrence graph if and only if their lowest common ancestor in the expression is a conjunction, [5] so the expression tree can be interpreted as a cotree for the corresponding cograph. [6]
Another alternative characterization of positive read-once functions combines their disjunctive and conjunctive normal form. A positive function of a given system of variables, that uses all of its variables, is read-once if and only if every prime implicant of the disjunctive normal form and every clause of the conjunctive normal form have exactly one variable in common. [7]
It is possible to recognize read-once functions from their disjunctive normal form expressions in polynomial time. [8] It is also possible to find a read-once expression for a positive read-once function, given access to the function only through a "black box" that allows its evaluation at any truth assignment, using only a quadratic number of function evaluations. [9]
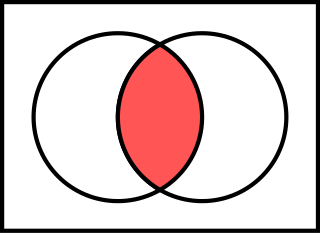
In logic, mathematics and linguistics, And is the truth-functional operator of logical conjunction; the and of a set of operands is true if and only if all of its operands are true. The logical connective that represents this operator is typically written as or ⋅ .
In logic, a logical connective is a logical constant used to connect two or more formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or a cluster concept. As a normal form, it is useful in automated theorem proving.
In Boolean logic, a formula is in conjunctive normal form (CNF) or clausal normal form if it is a conjunction of one or more clauses, where a clause is a disjunction of literals; otherwise put, it is a product of sums or an AND of ORs. As a canonical normal form, it is useful in automated theorem proving and circuit theory.
In mathematical logic, a formula is in negation normal form (NNF) if the negation operator is only applied to variables and the only other allowed Boolean operators are conjunction and disjunction.
In computer science, a binary decision diagram (BDD) or branching program is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed representation of sets or relations. Unlike other compressed representations, operations are performed directly on the compressed representation, i.e. without decompression. Other data structures used to represent Boolean functions include negation normal form (NNF), Zhegalkin polynomials, and propositional directed acyclic graphs (PDAG).
In mathematics, a Boolean function is a function whose arguments, as well as the function itself, assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
In Boolean algebra, the algebraic normal form (ANF), ring sum normal form, Zhegalkin normal form, or Reed–Muller expansion is a way of writing logical formulas in one of three subforms:
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.
In Boolean logic, a product term is a conjunction of literals, where each literal is either a variable or its negation.
In logic, a clause is an expression formed from a finite collection of literals. A clause is true either whenever at least one of the literals that form it is true, or when all of the literals that form it are true. That is, it is a finite disjunction or conjunction of literals, depending on the context. Clauses are usually written as follows, where the symbols are literals:
In logic, a functionally complete set of logical connectives or Boolean operators is one which can be used to express all possible truth tables by combining members of the set into a Boolean expression. A well-known complete set of connectives is { AND, NOT }, consisting of binary conjunction and negation. Each of the singleton sets { NAND } and { NOR } is functionally complete.
In mathematical logic, a literal is an atomic formula (atom) or its negation. The definition mostly appears in proof theory, e.g. in conjunctive normal form and the method of resolution.
In Boolean algebra, the consensus theorem or rule of consensus is the identity:
Zhegalkinpolynomials are a representation of functions in Boolean algebra. Introduced by the Russian mathematician Ivan Ivanovich Zhegalkin in 1927, they are the polynomial ring over the integers modulo 2. The resulting degeneracies of modular arithmetic result in Zhegalkin polynomials being simpler than ordinary polynomials, requiring neither coefficients nor exponents. Coefficients are redundant because 1 is the only nonzero coefficient. Exponents are redundant because in arithmetic mod 2, x2 = x. Hence a polynomial such as 3x2y5z is congruent to, and can therefore be rewritten as, xyz.
In database theory, a conjunctive query is a restricted form of first-order queries using the logical conjunction operator. Many first-order queries can be written as conjunctive queries. In particular, a large part of queries issued on relational databases can be expressed in this way. Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries do not share.
Decision lists are a representation for Boolean functions which can be easily learnable from examples. Single term decision lists are more expressive than disjunctions and conjunctions; however, 1-term decision lists are less expressive than the general disjunctive normal form and the conjunctive normal form.
The Tseytin transformation, alternatively written Tseitin transformation, takes as input an arbitrary combinatorial logic circuit and produces a boolean formula in conjunctive normal form (CNF), which can be solved by a CNF-SAT solver. The length of the formula is linear in the size of the circuit. Input vectors that make the circuit output "true" are in 1-to-1 correspondence with assignments that satisfy the formula. This reduces the problem of circuit satisfiability on any circuit to the satisfiability problem on 3-CNF formulas.
In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0, respectively. Instead of elementary algebra, where the values of the variables are numbers and the prime operations are addition and multiplication, the main operations of Boolean algebra are the conjunction (and) denoted as ∧, the disjunction (or) denoted as ∨, and the negation (not) denoted as ¬. It is thus a formalism for describing logical operations, in the same way that elementary algebra describes numerical operations.
