In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

The chromatic polynomial is a graph polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to study the four color problem. It was generalised to the Tutte polynomial by Hassler Whitney and W. T. Tutte, linking it to the Potts model of statistical physics.

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph and contains information about how the graph is connected. It is denoted by .

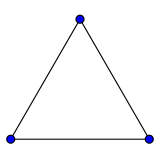
In the mathematical field of graph theory, the butterfly graph is a planar, undirected graph with 5 vertices and 6 edges. It can be constructed by joining 2 copies of the cycle graph C3 with a common vertex and is therefore isomorphic to the friendship graph F2.

In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the subgraph of G induced by all vertices adjacent to v, i.e., the graph composed of the vertices adjacent to v and all edges connecting vertices adjacent to v.

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of Jan Mycielski. The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number.

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.
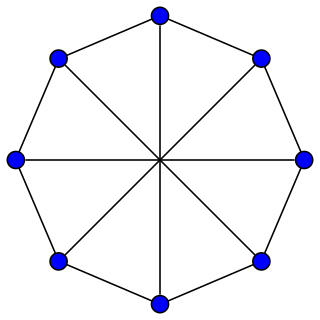
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.
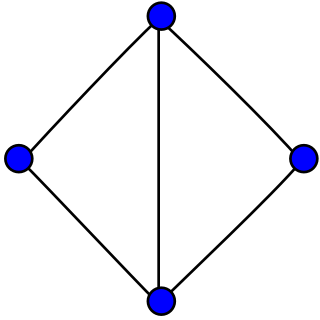
In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges. It consists of a complete graph minus one edge.

In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic.
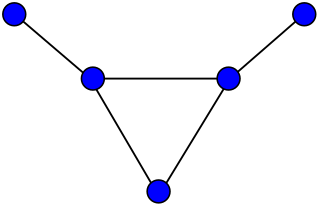
In the mathematical field of graph theory, the bull graph is a planar undirected graph with 5 vertices and 5 edges, in the form of a triangle with two disjoint pendant edges.

In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason, who used it to evaluate the Ramsey number R(3,3,3) = 17.

In the mathematical field of graph theory, the Brinkmann graph is a 4-regular graph with 21 vertices and 42 edges discovered by Gunnar Brinkmann in 1992. It was first published by Brinkmann and Meringer in 1997.

In the mathematical field of graph theory, the friendship graphFn is a planar, undirected graph with 2n + 1 vertices and 3n edges.

In mathematics, and particularly in graph theory, the dimension of a graph is the least integer n such that there exists a "classical representation" of the graph in the Euclidean space of dimension n with all the edges having unit length.