Girth (graph theory)

Last updated

In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. [1] If the graph does not contain any cycles (that is, it is a forest), its girth is defined to be infinity. [2] For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

Contents

Cages

A cubic graph (all vertices have degree three) of girth g that is as small as possible is known as a g-cage (or as a (3,g)-cage). The Petersen graph is the unique 5-cage (it is the smallest cubic graph of girth 5), the Heawood graph is the unique 6-cage, the McGee graph is the unique 7-cage and the Tutte eight cage is the unique 8-cage. [3] There may exist multiple cages for a given girth. For instance there are three nonisomorphic 10-cages, each with 70 vertices: the Balaban 10-cage, the Harries graph and the Harries–Wong graph.

Girth and graph coloring

For any positive integers g and χ, there exists a graph with girth at least g and chromatic number at least χ; for instance, the Grötzsch graph is triangle-free and has chromatic number 4, and repeating the Mycielskian construction used to form the Grötzsch graph produces triangle-free graphs of arbitrarily large chromatic number. Paul Erdős was the first to prove the general result, using the probabilistic method. [4] More precisely, he showed that a random graph on n vertices, formed by choosing independently whether to include each edge with probability n(1–g)/g, has, with probability tending to 1 as n goes to infinity, at most n⁄2 cycles of length g or less, but has no independent set of size n⁄2k. Therefore, removing one vertex from each short cycle leaves a smaller graph with girth greater than g, in which each color class of a coloring must be small and which therefore requires at least k colors in any coloring.

Explicit, though large, graphs with high girth and chromatic number can be constructed as certain Cayley graphs of linear groups over finite fields. [5] These remarkable Ramanujan graphs also have large expansion coefficient.

The odd girth and even girth of a graph are the lengths of a shortest odd cycle and shortest even cycle respectively.

The circumference of a graph is the length of the longest (simple) cycle, rather than the shortest.

Thought of as the least length of a non-trivial cycle, the girth admits natural generalisations as the 1-systole or higher systoles in systolic geometry.

Girth is the dual concept to edge connectivity, in the sense that the girth of a planar graph is the edge connectivity of its dual graph, and vice versa. These concepts are unified in matroid theory by the girth of a matroid, the size of the smallest dependent set in the matroid. For a graphic matroid, the matroid girth equals the girth of the underlying graph, while for a co-graphic matroid it equals the edge connectivity. [6]

Computation

The girth of an undirected graph can be computed by running a breadth-first search from each node, with complexity where is the number of vertices of the graph and is the number of edges. [7] A practical optimization is to limit the depth of the BFS to a depth that depends on the length of the smallest cycle discovered so far. [8] Better algorithms are known in the case where the girth is even [9] and when the graph is planar. [10] In terms of lower bounds, computing the girth of a graph is at least as hard as solving the triangle finding problem on the graph.

Related Research Articles

<span class="mw-page-title-main">Component (graph theory)</span> Maximal subgraph whose vertices can reach each other

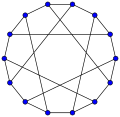
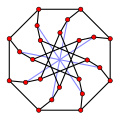
In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

<span class="mw-page-title-main">Graph coloring</span> Methodic assignment of colors to elements of a graph

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

<span class="mw-page-title-main">Edge coloring</span> Problem of coloring a graphs edges such that meeting edges do not match

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

<span class="mw-page-title-main">Snark (graph theory)</span> 3-regular graph with no 3-edge-coloring

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

<span class="mw-page-title-main">Connectivity (graph theory)</span> Basic concept of graph theory

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

<span class="mw-page-title-main">Graph property</span> Property of graphs that depends only on abstract structure

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

<span class="mw-page-title-main">Dual graph</span> Graph representing faces of another graph

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

<span class="mw-page-title-main">Tutte polynomial</span> Algebraic encoding of graph connectivity

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph and contains information about how the graph is connected. It is denoted by .

In graph theory, a Moore graph is a regular graph whose girth is more than twice its diameter. If the degree of such a graph is d and its diameter is k, its girth must equal 2k + 1. This is true, for a graph of degree d and diameter k, if and only if its number of vertices equals

In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

<span class="mw-page-title-main">Triangle-free graph</span> Graph without triples of adjacent vertices

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.

In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of Jan Mycielski (1955). The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number.

<span class="mw-page-title-main">Grötzsch graph</span> Triangle-free graph requiring four colors

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.

<span class="mw-page-title-main">Cage (graph theory)</span> Regular graph with fewest possible nodes for its girth

In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.

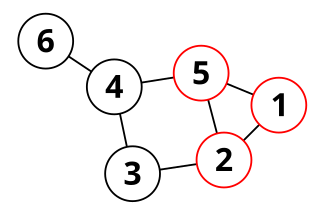
<span class="mw-page-title-main">Peripheral cycle</span> Graph cycle which does not separate remaining elements

In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.

<span class="mw-page-title-main">Chvátal graph</span>

In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic.

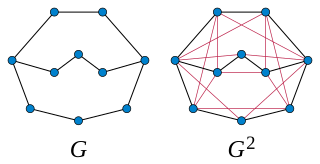
<span class="mw-page-title-main">Graph power</span> Graph operation: linking all pairs of nodes of distance ≤ k

In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.

In matroid theory, a mathematical discipline, the girth of a matroid is the size of its smallest circuit or dependent set. The cogirth of a matroid is the girth of its dual matroid. Matroid girth generalizes the notion of the shortest cycle in a graph, the edge connectivity of a graph, Hall sets in bipartite graphs, even sets in families of sets, and general position of point sets. It is hard to compute, but fixed-parameter tractable for linear matroids when parameterized both by the matroid rank and the field size of a linear representation.

References

  1. ↑ R. Diestel, Graph Theory, p.8. 3rd Edition, Springer-Verlag, 2005
  2. ↑ Weisstein, Eric W., "Girth", MathWorld
  3. ↑ Brouwer, Andries E., Cages . Electronic supplement to the book Distance-Regular Graphs (Brouwer, Cohen, and Neumaier 1989, Springer-Verlag).
  4. ↑ Erdős, Paul (1959), "Graph theory and probability", Canadian Journal of Mathematics, 11: 34–38, doi: 10.4153/CJM-1959-003-9 , S2CID   122784453 .
  5. ↑ Davidoff, Giuliana; Sarnak, Peter; Valette, Alain (2003), Elementary number theory, group theory, and Ramanujan graphs, London Mathematical Society Student Texts, vol. 55, Cambridge University Press, Cambridge, doi:10.1017/CBO9780511615825, ISBN   0-521-82426-5, MR   1989434
  6. ↑ Cho, Jung Jin; Chen, Yong; Ding, Yu (2007), "On the (co)girth of a connected matroid", Discrete Applied Mathematics, 155 (18): 2456–2470, doi: 10.1016/j.dam.2007.06.015 , MR   2365057 .
  7. ↑ https://web.archive.org/web/20170829175217if_/http://webcourse.cs.technion.ac.il/234247/Winter2003-2004/ho/WCFiles/Girth.pdf [ bare URL PDF ]
  8. ↑ Völkel, Christoph Dürr, Louis Abraham and Finn (2016-11-06). "Shortest cycle". TryAlgo. Retrieved 2023-02-22.{{cite web}}: CS1 maint: multiple names: authors list (link)
  9. ↑ "ds.algorithms - Optimal algorithm for finding the girth of a sparse graph?". Theoretical Computer Science Stack Exchange. Retrieved 2023-02-22.
  10. ↑ Chang, Hsien-Chih; Lu, Hsueh-I. (2013). "Computing the Girth of a Planar Graph in Linear Time". SIAM Journal on Computing. 42 (3): 1077–1094. arXiv: 1104.4892 . doi:10.1137/110832033. ISSN   0097-5397. S2CID   2493979.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.