In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 known cubic distance-regular graphs. It is named after Harold Scott MacDonald Coxeter.

In the mathematical field of graph theory, the Pappus graph is a bipartite, 3-regular, undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic, distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.

In the mathematical field of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.
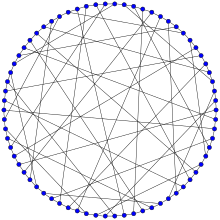
In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.
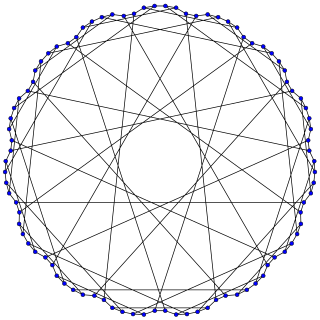
In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.

In the mathematical field of graph theory, the Balaban 10-cage or Balaban (3,10)-cage is a 3-regular graph with 70 vertices and 105 edges named after Alexandru T. Balaban. Published in 1972, It was the first 10-cage discovered but it is not unique.

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

In the mathematical field of graph theory, the Balaban 11-cage or Balaban (3,11)-cage is a 3-regular graph with 112 vertices and 168 edges named after Alexandru T. Balaban.

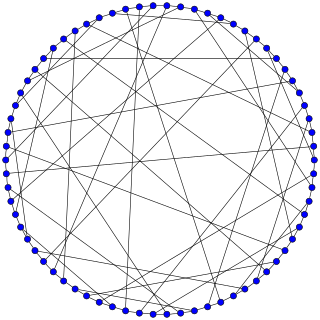
In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.
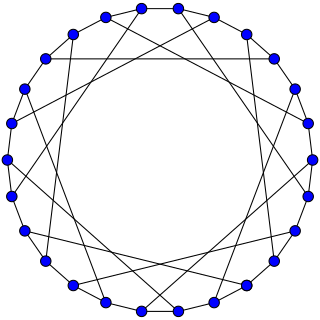
In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.

In the mathematical field of graph theory, the Horton graph or Horton 96-graph is a 3-regular graph with 96 vertices and 144 edges discovered by Joseph Horton. Published by Bondy and Murty in 1976, it provides a counterexample to the Tutte conjecture that every cubic 3-connected bipartite graph is Hamiltonian.

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges, rediscovered in 2002 and named after Ljubljana.
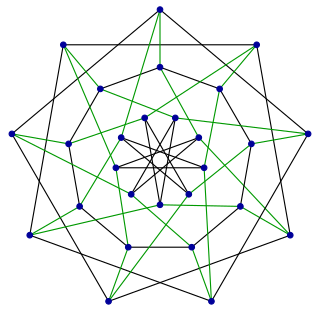
In graph theory, the Holt graph or Doyle graph is the smallest half-transitive graph, that is, the smallest example of a vertex-transitive and edge-transitive graph which is not also symmetric. Such graphs are not common. It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 and 1981 respectively.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges. It is named after W. T. Tutte.

In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.

The 110-vertex Iofinova–Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.