In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
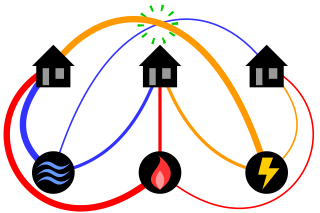
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .
In graph theory, two graphs and are homeomorphic if there is a graph isomorphism from some subdivision of to some subdivision of . If the edges of a graph are thought of as lines drawn from one vertex to another, then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if their diagrams are homeomorphic in the topological sense.
In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.
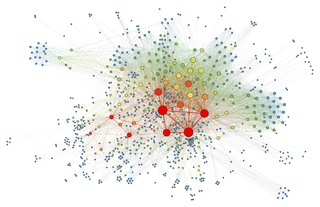
Force-directed graph drawing algorithms are a class of algorithms for drawing graphs in an aesthetically-pleasing way. Their purpose is to position the nodes of a graph in two-dimensional or three-dimensional space so that all the edges are of more or less equal length and there are as few crossing edges as possible, by assigning forces among the set of edges and the set of nodes, based on their relative positions, and then using these forces either to simulate the motion of the edges and nodes or to minimize their energy.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In combinatorial mathematics, rotation systems encode embeddings of graphs onto orientable surfaces by describing the circular ordering of a graph's edges around each vertex. A more formal definition of a rotation system involves pairs of permutations; such a pair is sufficient to determine a multigraph, a surface, and a 2-cell embedding of the multigraph onto the surface.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In the mathematical field of graph theory, Fáry's theorem states that any simple, planar graph can be drawn without crossings so that its edges are straight line segments. That is, the ability to draw graph edges as curves instead of as straight line segments does not allow a larger class of graphs to be drawn. The theorem is named after István Fáry, although it was proved independently by Klaus Wagner, Fáry, and Sherman K. Stein.
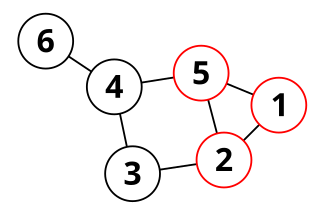
In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
A combinatorial map is a combinatorial representation of a graph on an orientable surface. A combinatorial map may also be called a combinatorial embedding, a rotation system, an orientable ribbon graph, a fat graph, or a cyclic graph. More generally, an -dimensional combinatorial map is a combinatorial representation of a graph on an -dimensional orientable manifold.
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.

In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold into topological disks such that every flag can be transformed into any other flag by a symmetry of the decomposition. Regular maps are, in a sense, topological generalizations of Platonic solids. The theory of maps and their classification is related to the theory of Riemann surfaces, hyperbolic geometry, and Galois theory. Regular maps are classified according to either: the genus and orientability of the supporting surface, the underlying graph, or the automorphism group.
The Fisher–Kasteleyn–Temperley (FKT) algorithm, named after Michael Fisher, Pieter Kasteleyn, and Neville Temperley, counts the number of perfect matchings in a planar graph in polynomial time. This same task is #P-complete for general graphs. For matchings that are not required to be perfect, counting them remains #P-complete even for planar graphs. The key idea of the FKT algorithm is to convert the problem into a Pfaffian computation of a skew-symmetric matrix derived from a planar embedding of the graph. The Pfaffian of this matrix is then computed efficiently using standard determinant algorithms.
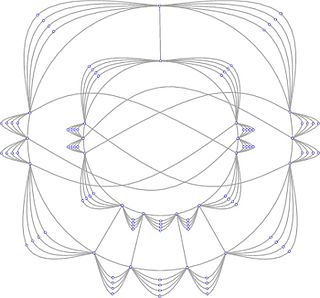
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.

An arc diagram is a style of graph drawing, in which the vertices of a graph are placed along a line in the Euclidean plane, with edges being drawn as semicircles in one or both of the two halfplanes bounded by the line, or as smooth curves formed by sequences of semicircles. In some cases, line segments of the line itself are also allowed as edges, as long as they connect only vertices that are consecutive along the line. Variations of this drawing style in which the semicircles are replaced by convex curves of some other type are also commonly called arc diagrams.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte, states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.

In graph drawing, an upward planar drawing of a directed acyclic graph is an embedding of the graph into the Euclidean plane, in which the edges are represented as non-crossing monotonic upwards curves. That is, the curve representing each edge should have the property that every horizontal line intersects it in at most one point, and no two edges may intersect except at a shared endpoint. In this sense, it is the ideal case for layered graph drawing, a style of graph drawing in which edges are monotonic curves that may cross, but in which crossings are to be minimized.
























