In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its even-degree subgraphs.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices, thus it is "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.
In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the subgraph of G induced by all vertices adjacent to v, i.e., the graph composed of the vertices adjacent to v and all edges connecting vertices adjacent to v.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

In graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and more specifically graph algorithms, to represent the triconnected components of a graph. The SPQR tree of a graph may be constructed in linear time and has several applications in dynamic graph algorithms and graph drawing.
In graph theory, the planarity testing problem is the algorithmic problem of testing whether a given graph is a planar graph (that is, whether it can be drawn in the plane without edge intersections). This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures. Most of these methods operate in O(n) time (linear time), where n is the number of edges (or vertices) in the graph, which is asymptotically optimal. Rather than just being a single Boolean value, the output of a planarity testing algorithm may be a planar graph embedding, if the graph is planar, or an obstacle to planarity such as a Kuratowski subgraph if it is not.
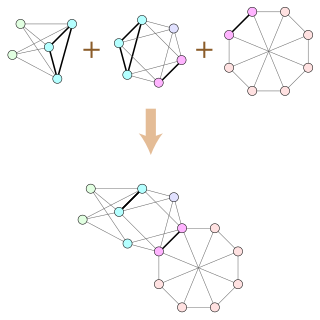
In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have at most k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the two-graph clique-sum operation.

Clique complexes, independence complexes, flag complexes, Whitney complexes and conformal hypergraphs are closely related mathematical objects in graph theory and geometric topology that each describe the cliques of an undirected graph.
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and Paul Seymour. Its proof is very long and involved. Kawarabayashi & Mohar (2007) and Lovász (2006) are surveys accessible to nonspecialists, describing the theorem and its consequences.
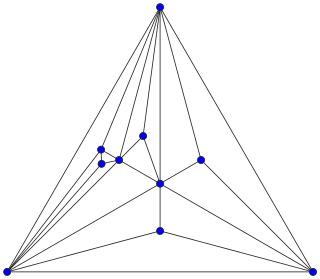
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Equivalently, these are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.