In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
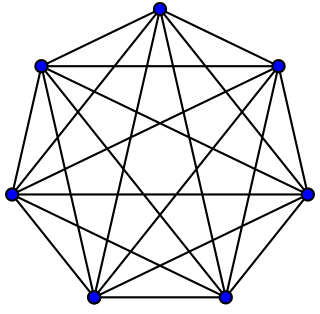
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.

In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that is closed under minors can be defined by a finite set of forbidden minors, in the same way that Wagner's theorem characterizes the planar graphs as being the graphs that do not have the complete graph K5 or the complete bipartite graph K3,3 as minors.
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.
In graph theory, two graphs and are homeomorphic if there is a graph isomorphism from some subdivision of to some subdivision of . If the edges of a graph are thought of as lines drawn from one vertex to another, then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if their diagrams are homeomorphic in the topological sense.
In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph. The distinction of what constitutes a dense or sparse graph is ill-defined, and is often represented by 'roughly equal to' statements. Due to this, the way that density is defined often depends on the context of the problem.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

In complexity theory and graph theory, induced subgraph isomorphism is an NP-complete decision problem that involves finding a given graph as an induced subgraph of a larger graph.

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
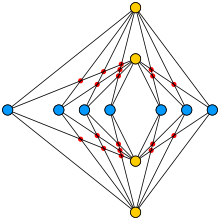
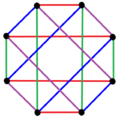
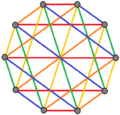
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices {u1, u2, …, un} and {v1, v2, …, vn} and with an edge from ui to vj whenever i ≠ j.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.
In graph theory, a branch of mathematics, a t-biclique-free graph is a graph that has no Kt,t as a subgraph. A family of graphs is biclique-free if there exists a number t such that the graphs in the family are all t-biclique-free. The biclique-free graph families form one of the most general types of sparse graph family. They arise in incidence problems in discrete geometry, and have also been used in parameterized complexity.