
In mathematics, the Borsuk–Ulam theorem states that every continuous function from an n-sphere into Euclidean n-space maps some pair of antipodal points to the same point. Here, two points on a sphere are called antipodal if they are in exactly opposite directions from the sphere's center.
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial complex from an abstract simplicial complex, the former is often called a geometric simplicial complex.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

In combinatorics, an abstract simplicial complex (ASC), often called an abstract complex or just a complex, is a family of sets that is closed under taking subsets, i.e., every subset of a set in the family is also in the family. It is a purely combinatorial description of the geometric notion of a simplicial complex. For example, in a 2-dimensional simplicial complex, the sets in the family are the triangles, their edges, and their vertices.

In geometry, Radon's theorem on convex sets, published by Johann Radon in 1921, states that:
Any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect.

In graph theory, the Kneser graphK(n, k) (alternatively KGn,k) is the graph whose vertices correspond to the k-element subsets of a set of n elements, and where two vertices are adjacent if and only if the two corresponding sets are disjoint. Kneser graphs are named after Martin Kneser, who first investigated them in 1956.

In mathematics, Tucker's lemma is a combinatorial analog of the Borsuk–Ulam theorem, named after Albert W. Tucker.
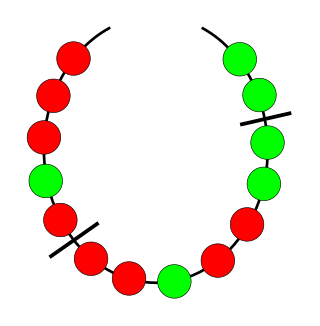
Necklace splitting is a picturesque name given to several related problems in combinatorics and measure theory. Its name and solutions are due to mathematicians Noga Alon and Douglas B. West.

Jiří (Jirka) Matoušek was a Czech mathematician working in computational geometry and algebraic topology. He was a professor at Charles University in Prague and the author of several textbooks and research monographs.
In geometry, the moment curve is an algebraic curve in d-dimensional Euclidean space given by the set of points with Cartesian coordinates of the form
In mathematics, equivariant topology is the study of topological spaces that possess certain symmetries. In studying topological spaces, one often considers continuous maps , and while equivariant topology also considers such maps, there is the additional constraint that each map "respects symmetry" in both its domain and target space.

Dmitry Feichtner-Kozlov is a Russian-German mathematician.
Using the Borsuk–Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry is a graduate-level mathematics textbook in topological combinatorics. It describes the use of results in topology, and in particular the Borsuk–Ulam theorem, to prove theorems in combinatorics and discrete geometry. It was written by Czech mathematician Jiří Matoušek, and published in 2003 by Springer-Verlag in their Universitext series (ISBN 978-3-540-00362-5).
A chessboard complex is a particular kind of abstract simplicial complex, which has various applications in topological graph theory and algebraic topology. Informally, the (m, n)-chessboard complex contains all sets of positions on an m-by-n chessboard, where rooks can be placed without attacking each other. Equivalently, it is the matching complex of the (m, n)-complete bipartite graph, or the independence complex of the m-by-n rook's graph.


















