
A Venn diagram is a widely used diagram style that shows the logical relation between sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses simple closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses.

In computer science, binary space partitioning (BSP) is a method for space partitioning which recursively subdivides a Euclidean space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to a representation of objects within the space in the form of a tree data structure known as a BSP tree.
The Gödel Prize is an annual prize for outstanding papers in the area of theoretical computer science, given jointly by the European Association for Theoretical Computer Science (EATCS) and the Association for Computing Machinery Special Interest Group on Algorithms and Computational Theory. The award is named in honor of Kurt Gödel. Gödel's connection to theoretical computer science is that he was the first to mention the "P versus NP" question, in a 1956 letter to John von Neumann in which Gödel asked whether a certain NP-complete problem could be solved in quadratic or linear time.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.
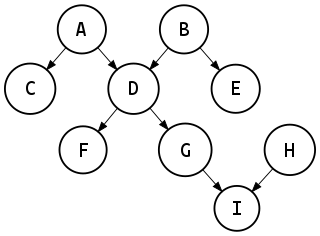
In mathematics, and more specifically in graph theory, a polytree is a directed acyclic graph whose underlying undirected graph is a tree. In other words, if we replace its directed edges with undirected edges, we obtain an undirected graph that is both connected and acyclic.
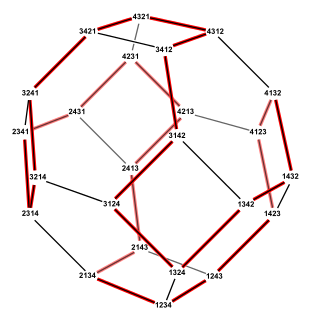
The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of elements. Each permutation in the sequence that it generates differs from the previous permutation by swapping two adjacent elements of the sequence. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron.
In mathematics, in the areas of combinatorics and computer science, a Lyndon word is a nonempty string that is strictly smaller in lexicographic order than all of its rotations. Lyndon words are named after mathematician Roger Lyndon, who investigated them in 1954, calling them standard lexicographic sequences. Anatoly Shirshov introduced Lyndon words in 1953 calling them regular words. Lyndon words are a special case of Hall words; almost all properties of Lyndon words are shared by Hall words.
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

David Arthur Eppstein is an American computer scientist and mathematician. He is a Distinguished Professor of computer science at the University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics. In 2011, he was named an ACM Fellow.
In graph theory and computer science, the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest node that has both v and w as descendants, where we define each node to be a descendant of itself.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

Kurt Mehlhorn is a German theoretical computer scientist. He has been a vice president of the Max Planck Society and is director of the Max Planck Institute for Computer Science.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be small for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i (denoted by i(v))
- Disjoint union of two labeled graphs G and H (denoted by )
- Joining by an edge every vertex labeled i to every vertex labeled j (denoted by η(i,j)), where i ≠ j
- Renaming label i to label j (denoted by ρ(i,j))
In graph theory and theoretical computer science, the longest path problem is the problem of finding a simple path of maximum length in a given graph. A path is called simple if it does not have any repeated vertices; the length of a path may either be measured by its number of edges, or by the sum of the weights of its edges. In contrast to the shortest path problem, which can be solved in polynomial time in graphs without negative-weight cycles, the longest path problem is NP-hard and the decision version of the problem, which asks whether a path exists of at least some given length, is NP-complete. This means that the decision problem cannot be solved in polynomial time for arbitrary graphs unless P = NP. Stronger hardness results are also known showing that it is difficult to approximate. However, it has a linear time solution for directed acyclic graphs, which has important applications in finding the critical path in scheduling problems.
Michael Ezra Saks is an American mathematician. He is currently the Department Chair of the Mathematics Department at Rutgers University (2017–) and from 2006 until 2010 was director of the Mathematics Graduate Program at Rutgers University. Saks received his Ph.D. from the Massachusetts Institute of Technology in 1980 after completing his dissertation titled Duality Properties of Finite Set Systems under his advisor Daniel J. Kleitman.

In applied mathematics, a bit-reversal permutation is a permutation of a sequence of items, where is a power of two. It is defined by indexing the elements of the sequence by the numbers from to , representing each of these numbers by its binary representation, and mapping each item to the item whose representation has the same bits in the reversed order.
Carla Diane Savage is an American computer scientist and mathematician, a professor of computer science at North Carolina State University and a former secretary of the American Mathematical Society (2013-2020).

Gad Menahem Landau is an Israeli computer scientist noted for his contributions to combinatorial pattern matching and string algorithms and is the founding department chair of the Computer Science Department at the University of Haifa.













