Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).

The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, followed closely by Ancient Egypt and the Levantine state of Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the field of astronomy to record time and formulate calendars.

Zhu Shijie, courtesy name Hanqing (漢卿), pseudonym Songting (松庭), was a Chinese mathematician and writer during the Yuan Dynasty. Zhu was born close to today's Beijing. Two of his mathematical works have survived: Introduction to Computational Studies and Jade Mirror of the Four Unknowns.

Zu Chongzhi, courtesy name Wenyuan, was a Chinese astronomer, inventor, mathematician, politician, and writer during the Liu Song and Southern Qi dynasties. He was most notable for calculating pi as between 3.1415926 and 3.1415927, a record in precision which would not be surpassed for nearly 900 years.

Liu Hui was a Chinese mathematician who published a commentary in 263 CE on Jiu Zhang Suan Shu. He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state of Cao Wei during the Three Kingdoms period of China.

The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE. This book is one of the earliest surviving mathematical texts from China, the others being the Suan shu shu and Zhoubi Suanjing. It lays out an approach to mathematics that centres on finding the most general methods of solving problems, which may be contrasted with the approach common to ancient Greek mathematicians, who tended to deduce propositions from an initial set of axioms.

Seki Takakazu, also known as Seki Kōwa, was a Japanese mathematician and author of the Edo period.

Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system, algebra, geometry, number theory and trigonometry.
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the nth polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members.
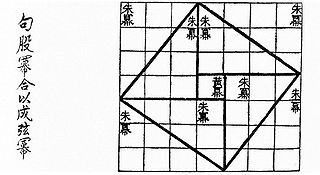
The Zhoubi Suanjing, also known by many other names, is an ancient Chinese astronomical and mathematical work. The Zhoubi is most famous for its presentation of Chinese cosmology and a form of the Pythagorean theorem. It claims to present 246 problems worked out by the Duke of Zhou as well as members of his court, placing its composition during the 11th century BC. However, the present form of the book does not seem to be earlier than the Eastern Han (25–220 AD), with some additions and commentaries continuing to be added for several more centuries.

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function, cosine function, and versine function.

Ancient Chinese scientists and engineers made significant scientific innovations, findings and technological advances across various scientific disciplines including the natural sciences, engineering, medicine, military technology, mathematics, geology and astronomy.

Ghiyāth al-Dīn Jamshīd Masʿūd al-Kāshī was an astronomer and mathematician during the reign of Tamerlane.

Magic circles were invented by the Song dynasty (960–1279) Chinese mathematician Yang Hui. It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameters are identical. One of his magic circles was constructed from the natural numbers from 1 to 33 arranged on four concentric circles, with 9 at the center.
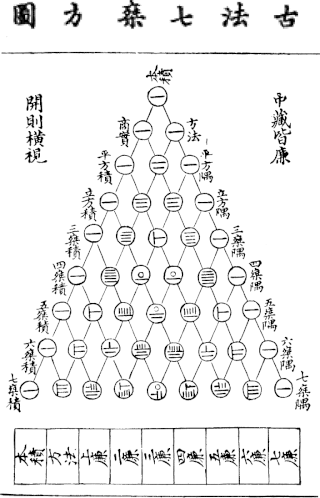
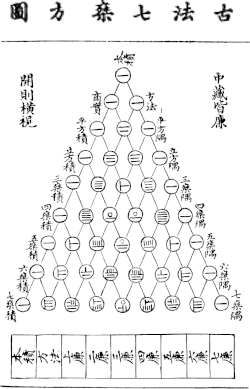
Jia Xian was a Chinese mathematician from Kaifeng of the Song dynasty. He described Pascal's triangle during the 11th century.
The mathematical field of combinatorics was studied to varying degrees in numerous ancient societies. Its study in Europe dates to the work of Leonardo Fibonacci in the 13th century AD, which introduced Arabian and Indian ideas to the continent. It has continued to be studied in the modern era.
Li Ye, born Li Zhi, courtesy name Li Jingzhai, was a Chinese mathematician, politician, and writer who published and improved the tian yuan shu method for solving polynomial equations of one variable. Along with the 4th-century Chinese astronomer Yu Xi, Li Ye proposed the idea of a spherical Earth instead of a flat one before the advances of European science in the 17th century.

Cheng Dawei, also known as Da Wei Cheng or Ch'eng Ta-wei, was a Chinese mathematician and writer who was known mainly as the author of Suanfa Tongzong (算法統宗). He has been described as "the most illustrious Chinese arithmetician."
Suanfa tongzong is a mathematical text written by sixteenth century Chinese mathematician Cheng Dawei (1533–1606) and published in the year 1592. The book contains 595 problems divided into 17 chapters. The book is essentially general arithmetic for the abacus. The book was the main source available to scholars concerning mathematics as it developed in China's tradition. Six years after the publication of Suanfa Tongzong, Cheng Dawei published another book titled Suanfa Zuanyao. About 90% of the content of the new book came from the contents of four chapters of the first book with some rearrangement. It is said that when Suanfa Tongzong was first published, it sold so many copies that the cost of paper went up and the lucrative sales resulted in unscrupulous people beginning to print pirated copies of the book with many errors. It was this that forced the author to print an abridged version.