
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.

In geometry, a hypotenuse is the side of a right triangle opposite the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called catheti or legs. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two legs. Mathematically, this can be written as , where a is the length of one leg, b is the length of another leg, and c is the length of the hypotenuse.

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
Divine Proportions: Rational Trigonometry to Universal Geometry is a 2005 book by the mathematician Norman J. Wildberger on a proposed alternative approach to Euclidean geometry and trigonometry, called rational trigonometry. The book advocates replacing the usual basic quantities of trigonometry, Euclidean distance and angle measure, by squared distance and the square of the sine of the angle, respectively. This is logically equivalent to the standard development. The author claims his approach holds some advantages, such as avoiding the need for irrational numbers.
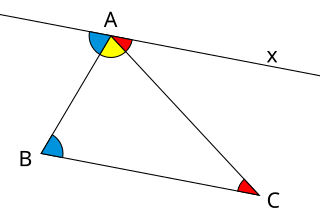
In a Euclidean space, the sum of angles of a triangle equals a straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

The following outline is provided as an overview of and topical guide to trigonometry:
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a geometer. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts.
The following is a timeline of key developments of geometry:
This is a timeline of pure and applied mathematics history. It is divided here into three stages, corresponding to stages in the development of mathematical notation: a "rhetorical" stage in which calculations are described purely by words, a "syncopated" stage in which quantities and common algebraic operations are beginning to be represented by symbolic abbreviations, and finally a "symbolic" stage, in which comprehensive notational systems for formulas are the norm.
In geometry, a Schläfli orthoscheme is a type of simplex. The orthoscheme is the generalization of the right triangle to simplex figures of any number of dimensions. Orthoschemes are defined by a sequence of edges that are mutually orthogonal. They were introduced by Ludwig Schläfli, who called them orthoschemes and studied their volume in Euclidean, hyperbolic, and spherical geometries. H. S. M. Coxeter later named them after Schläfli. As right triangles provide the basis for trigonometry, orthoschemes form the basis of a trigonometry of n dimensions, as developed by Schoute who called it polygonometry. J.-P. Sydler and Børge Jessen studied orthoschemes extensively in connection with Hilbert's third problem.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.
In geometry, it is an unsolved conjecture of Hugo Hadwiger that every simplex can be dissected into orthoschemes, using a number of orthoschemes bounded by a function of the dimension of the simplex. If true, then more generally every convex polytope could be dissected into orthoschemes.

In three-dimensional hyperbolic geometry, an ideal polyhedron is a convex polyhedron all of whose vertices are ideal points, points "at infinity" rather than interior to three-dimensional hyperbolic space. It can be defined as the convex hull of a finite set of ideal points. An ideal polyhedron has ideal polygons as its faces, meeting along lines of the hyperbolic space.











