Polar sine

Last updated January 25, 2024

In geometry, the polar sine generalizes the sine function of angle to the vertex angle of a polytope. It is denoted by psin.

Definition

n vectors in n-dimensional space

Let v₁, ..., v_n (n ≥ 1) be non-zero Euclidean vectors in n-dimensional space (Rⁿ) that are directed from a vertex of a parallelotope, forming the edges of the parallelotope. The polar sine of the vertex angle is:

\operatorname {psin} (\mathbf {v} _{1},\dots ,\mathbf {v} _{n})={\frac {\Omega }{\Pi }},

where the numerator is the determinant

{\begin{aligned}\Omega &=\det {\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}={\begin{vmatrix}v_{11}&v_{21}&\cdots &v_{n1}\\v_{12}&v_{22}&\cdots &v_{n2}\\\vdots &\vdots &\ddots &\vdots \\v_{1n}&v_{2n}&\cdots &v_{nn}\\\end{vmatrix}}\end{aligned}}\,,

which equals the signed hypervolume of the parallelotope with vector edges^[1]

{\begin{aligned}\mathbf {v} _{1}&=(v_{11},v_{12},\dots ,v_{1n})^{T}\\\mathbf {v} _{2}&=(v_{21},v_{22},\dots ,v_{2n})^{T}\\&\,\,\,\vdots \\\mathbf {v} _{n}&=(v_{n1},v_{n2},\dots ,v_{nn})^{T}\,,\\\end{aligned}}

and where the denominator is the n-fold product

\Pi =\prod _{i=1}^{n}\|\mathbf {v} _{i}\|

of the magnitudes of the vectors, which equals the hypervolume of the n-dimensional hyperrectangle with edges equal to the magnitudes of the vectors ||v₁||, ||v₂||, ... ||v_n|| rather than the vectors themselves. Also see Ericksson.^[2]

The parallelotope is like a "squashed hyperrectangle", so it has less hypervolume than the hyperrectangle, meaning (see image for the 3d case):

|\Omega |\leq \Pi \implies {\frac {|\Omega |}{\Pi }}\leq 1\implies -1\leq \operatorname {psin} (\mathbf {v} _{1},\dots ,\mathbf {v} _{n})\leq 1\,,

as for the ordinary sine, with either bound being reached only in the case that all vectors are mutually orthogonal.

In the case n = 2, the polar sine is the ordinary sine of the angle between the two vectors.

In higher dimensions

A non-negative version of the polar sine that works in any $m$ -dimensional space can be defined using the Gram determinant. It is a ratio where the denominator is as described above. The numerator is

|\Omega |={\sqrt {\det \left({\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}^{T}{\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}\right)}}\,,

where the superscript T indicates matrix transposition. This can be nonzero only if $m \geq n$ . In the case m = n, this is equivalent to the absolute value of the definition given previously. In the degenerate case $m < n$ , the determinant will be of a singular $n \times n$ matrix, giving $Ω = 0$ and $psin = 0$ , because it is not possible to have $n$ linearly independent vectors in $m$ -dimensional space when $m < n$ .

Properties

Interchange of vectors

The polar sine changes sign whenever two vectors are interchanged, due to the antisymmetry of row-exchanging in the determinant; however, its absolute value will remain unchanged.

{\begin{aligned}\Omega &=\det {\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{i}&\cdots &\mathbf {v} _{j}&\cdots &\mathbf {v} _{n}\end{bmatrix}}\\&=-\!\det {\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{j}&\cdots &\mathbf {v} _{i}&\cdots &\mathbf {v} _{n}\end{bmatrix}}\\&=-\Omega \end{aligned}}

Invariance under scalar multiplication of vectors

The polar sine does not change if all of the vectors v₁, ..., v_n are scalar-multiplied by positive constants c_i, due to factorization

{\begin{aligned}\operatorname {psin} (c_{1}\mathbf {v} _{1},\dots ,c_{n}\mathbf {v} _{n})&={\frac {\det {\begin{bmatrix}c_{1}\mathbf {v} _{1}&c_{2}\mathbf {v} _{2}&\cdots &c_{n}\mathbf {v} _{n}\end{bmatrix}}}{\prod _{i=1}^{n}\|c_{i}\mathbf {v} _{i}\|}}\\[6pt]&={\frac {\prod _{i=1}^{n}c_{i}}{\prod _{i=1}^{n}|c_{i}|}}\cdot {\frac {\det {\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}}{\prod _{i=1}^{n}\|\mathbf {v} _{i}\|}}\\[6pt]&=\operatorname {psin} (\mathbf {v} _{1},\dots ,\mathbf {v} _{n}).\end{aligned}}

If an odd number of these constants are instead negative, then the sign of the polar sine will change; however, its absolute value will remain unchanged.

Vanishes with linear dependencies

If the vectors are not linearly independent, the polar sine will be zero. This will always be so in the degenerate case that the number of dimensions $m$ is strictly less than the number of vectors $n$ .

Relationship to pairwise cosines

The cosine of the angle between two non-zero vectors is given by

\cos(\mathbf {v} _{1},\mathbf {v} _{2})={\frac {\mathbf {v} _{1}\cdot \mathbf {v} _{2}}{\|\mathbf {v} _{1}\|\|\mathbf {v} _{2}\|}}\,

using the dot product. Comparison of this expression to the definition of the absolute value of the polar sine as given above gives:

\left|\operatorname {psin} (\mathbf {v} _{1},\ldots ,\mathbf {v} _{n})\right|^{2}=\det \!\left[{\begin{matrix}1&\cos(\mathbf {v} _{1},\mathbf {v} _{2})&\cdots &\cos(\mathbf {v} _{1},\mathbf {v} _{n})\\\cos(\mathbf {v} _{2},\mathbf {v} _{1})&1&\cdots &\cos(\mathbf {v} _{2},\mathbf {v} _{n})\\\vdots &\vdots &\ddots &\vdots \\\cos(\mathbf {v} _{n},\mathbf {v} _{1})&\cos(\mathbf {v} _{n},\mathbf {v} _{2})&\cdots &1\\\end{matrix}}\right].

In particular, for $n = 2$ , this is equivalent to

\sin ^{2}(\mathbf {v} _{1},\mathbf {v} _{2})=1-\cos ^{2}(\mathbf {v} _{1},\mathbf {v} _{2})\,,

which is the Pythagorean theorem.

History

Polar sines were investigated by Euler in the 18th century.^[3]

Related Research Articles

In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. The determinant of a matrix $A$ is commonly denoted $det(A)$ , $det A$ , or $| A |$ . Its value characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants.

In mathematical physics and mathematics, the Pauli matrices are a set of three $2 \times 2$ complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.

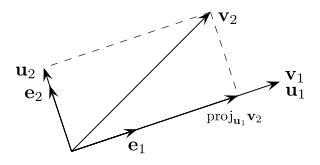
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of making two or more vectors perpendicular to each other.

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,

In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.

In mathematics, the cross product or vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space, and is denoted by the symbol $. Given two linearly independent vectors a and b, the cross product, a \times b, is a vector that is perpendicular to both a and b, and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product.$

In linear algebra, the adjugate or classical adjoint of a square matrix $A$ is the transpose of its cofactor matrix and is denoted by $adj(A)$ . It is also occasionally known as adjunct matrix, or "adjoint", though the latter term today normally refers to a different concept, the adjoint operator which for a matrix is the conjugate transpose.

In linear algebra, a QR decomposition, also known as a QR factorization or QU factorization, is a decomposition of a matrix A into a product A = QR of an orthonormal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares (LLS) problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.

In linear algebra, a circulant matrix is a square matrix in which all rows are composed of the same elements and each row is rotated one element to the right relative to the preceding row. It is a particular kind of Toeplitz matrix.

In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various partial derivatives of a single function with respect to many variables, and/or of a multivariate function with respect to a single variable, into vectors and matrices that can be treated as single entities. This greatly simplifies operations such as finding the maximum or minimum of a multivariate function and solving systems of differential equations. The notation used here is commonly used in statistics and engineering, while the tensor index notation is preferred in physics.

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.

In numerical linear algebra, the Jacobi method is an iterative algorithm for determining the solutions of a strictly diagonally dominant system of linear equations. Each diagonal element is solved for, and an approximate value is plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization. The method is named after Carl Gustav Jacob Jacobi.

In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.

In the mathematical discipline of matrix theory, a Jordan matrix, named after Camille Jordan, is a block diagonal matrix over a ring $R$ , where each block along the diagonal, called a Jordan block, has the following form:

In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.

In probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed. When determining the numerical relationship between two variables of interest, using their correlation coefficient will give misleading results if there is another confounding variable that is numerically related to both variables of interest. This misleading information can be avoided by controlling for the confounding variable, which is done by computing the partial correlation coefficient. This is precisely the motivation for including other right-side variables in a multiple regression; but while multiple regression gives unbiased results for the effect size, it does not give a numerical value of a measure of the strength of the relationship between the two variables of interest.

In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector $e$ indicating the direction (geometry) of an axis of rotation, and an angle of rotation $θ$ describing the magnitude and sense of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector $e$ rooted at the origin because the magnitude of $e$ is constrained. For example, the elevation and azimuth angles of $e$ suffice to locate it in any particular Cartesian coordinate frame.

In mathematics, specifically multilinear algebra, a dyadic or dyadic tensor is a second order tensor, written in a notation that fits in with vector algebra.

In analytical mechanics, the mass matrix is a symmetric matrix $M$ that expresses the connection between the time derivative $of the generalized coordinate vector q of a system and the kinetic energy T of that system, by the equation$

References

↑ Lerman, Gilad; Whitehouse, J. Tyler (2009). "On d-dimensional d-semimetrics and simplex-type inequalities for high-dimensional sine functions". Journal of Approximation Theory. 156: 52–81. arXiv: 0805.1430 . doi:10.1016/j.jat.2008.03.005. S2CID 12794652.
↑ Eriksson, F (1978). "The Law of Sines for Tetrahedra and n-Simplices". Geometriae Dedicata. 7: 71–80. doi:10.1007/bf00181352. S2CID 120391200.
↑ Euler, Leonhard. "De mensura angulorum solidorum". Leonhardi Euleri Opera Omnia. 26: 204–223.

External links

Weisstein, Eric W. "Polar Sine". MathWorld .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Lerman, Gilad; Whitehouse, J. Tyler (2009). "On d-dimensional d-semimetrics and simplex-type inequalities for high-dimensional sine functions". Journal of Approximation Theory. 156: 52–81. arXiv: 0805.1430 . doi:10.1016/j.jat.2008.03.005. S2CID 12794652.

[2] Eriksson, F (1978). "The Law of Sines for Tetrahedra and n-Simplices". Geometriae Dedicata. 7: 71–80. doi:10.1007/bf00181352. S2CID 120391200.

[3] Euler, Leonhard. "De mensura angulorum solidorum". Leonhardi Euleri Opera Omnia. 26: 204–223.

[1]

[2]

[3]