Notation
In this article, f denotes a real-valued function on which is periodic with period 2L.
In mathematics, particularly the field of calculus and Fourier analysis, the Fourier sine and cosine series are two mathematical series named after Joseph Fourier.
In this article, f denotes a real-valued function on which is periodic with period 2L.
If f is an odd function with period , then the Fourier Half Range sine series of f is defined to be which is just a form of complete Fourier series with the only difference that and are zero, and the series is defined for half of the interval.
In the formula we have
If f is an even function with a period , then the Fourier cosine series is defined to be where
This notion can be generalized to functions which are not even or odd, but then the above formulas will look different.

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that takes a function as input and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.

A Fourier series is an expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series, but not all trigonometric series are Fourier series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always converge. Well-behaved functions, for example smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric functions, described in Common forms of the Fourier series below.

A periodic function also called a periodic waveform, is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a cycle. For example, the trigonometric functions, which repeat at intervals of radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called aperiodic.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.

In mathematics, trigonometric integrals are a family of nonelementary integrals involving trigonometric functions.
In mathematics, the Gibbs phenomenon is the oscillatory behavior of the Fourier series of a piecewise continuously differentiable periodic function around a jump discontinuity. The th partial Fourier series of the function produces large peaks around the jump which overshoot and undershoot the function values. As more sinusoids are used, this approximation error approaches a limit of about 9% of the jump, though the infinite Fourier series sum does eventually converge almost everywhere except points of discontinuity.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions, under suitably restricted domains. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

In mathematics, the Clausen function, introduced by Thomas Clausen, is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.
In mathematics, orthogonal functions belong to a function space that is a vector space equipped with a bilinear form. When the function space has an interval as the domain, the bilinear form may be the integral of the product of functions over the interval:

In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:

In mathematics, a series expansion is a technique that expresses a function as an infinite sum, or series, of simpler functions. It is a method for calculating a function that cannot be expressed by just elementary operators.

In mathematics, the Fourier sine and cosine transforms are integral equations that decompose arbitrary functions into a sum of sine waves representing the odd component of the function plus cosine waves representing the even component of the function. The modern Fourier transform concisely contains both the sine and cosine transforms. Since the sine and cosine transforms use sine and cosine waves instead of complex exponentials and don't require complex numbers or negative frequency, they more closely correspond to Joseph Fourier's original transform equations and are still preferred in some signal processing and statistics applications and may be better suited as an introduction to Fourier analysis.
In mathematics, a half range Fourier series is a Fourier series defined on an interval instead of the more common , with the implication that the analyzed function should be extended to as either an even or odd function. This allows the expansion of the function in a series solely of sines (odd) or cosines (even). The choice between odd and even is typically motivated by boundary conditions associated with a differential equation satisfied by .

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others.
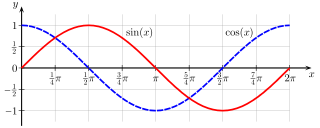
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted as and .
Clenshaw–Curtis quadrature and Fejér quadrature are methods for numerical integration, or "quadrature", that are based on an expansion of the integrand in terms of Chebyshev polynomials. Equivalently, they employ a change of variables and use a discrete cosine transform (DCT) approximation for the cosine series. Besides having fast-converging accuracy comparable to Gaussian quadrature rules, Clenshaw–Curtis quadrature naturally leads to nested quadrature rules, which is important for both adaptive quadrature and multidimensional quadrature (cubature).
In the 1760s, Johann Heinrich Lambert was the first to prove that the number π is irrational, meaning it cannot be expressed as a fraction , where and are both integers. In the 19th century, Charles Hermite found a proof that requires no prerequisite knowledge beyond basic calculus. Three simplifications of Hermite's proof are due to Mary Cartwright, Ivan Niven, and Nicolas Bourbaki. Another proof, which is a simplification of Lambert's proof, is due to Miklós Laczkovich. Many of these are proofs by contradiction.

In mathematical analysis, the Dirichlet kernel, named after the German mathematician Peter Gustav Lejeune Dirichlet, is the collection of periodic functions defined as