Related Research Articles
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to information science to computation (scheduling).
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
In graph theory, an Eulerian trail is a trail in a finite graph that visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this:
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.
In mathematics, an incidence matrix is a logical matrix that shows the relationship between two classes of objects, usually called an incidence relation. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related and 0 if they are not. There are variations; see below.
In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.
In discrete mathematics, and more specifically in graph theory, a vertex or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges, while a directed graph consists of a set of vertices and a set of arcs. In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.
In the mathematical discipline of graph theory, a graph labelling is the assignment of labels, traditionally represented by integers, to edges and/or vertices of a graph.
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition. These edges are said to cross the cut. In a connected graph, each cut-set determines a unique cut, and in some cases cuts are identified with their cut-sets rather than with their vertex partitions.
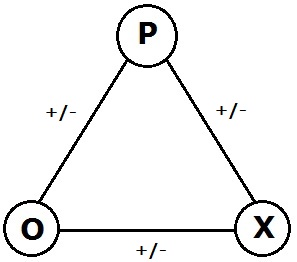
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.
In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
In graph theory, a voltage graph is a directed graph whose edges are labelled invertibly by elements of a group. It is formally identical to a gain graph, but it is generally used in topological graph theory as a concise way to specify another graph called the derived graph of the voltage graph.
In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
References
- ↑ Kwong, Harris; Lee, Sin-Min; Ng, Ho (2008). "On friendly index sets of 2-regular graphs". Discrete Math. 308 (23): 5522–5532. doi: 10.1016/j.disc.2007.10.018 . MR 2459372.
- ↑ Gallian, Joseph A (2009). "A dynamic survey of graph labelling" (PDF). El. J. Combinat. 16 (#DS6).
 | This graph theory-related article is a stub. You can help Wikipedia by expanding it. |