
In mathematics, an exponential function is a function of the form
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.

In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For any positive integer

In mathematics, the Laplace transform, named after its inventor Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms differential equations into algebraic equations and convolution into multiplication.

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x), or log(x). This is done in particular when the argument to the logarithm is not a single symbol, to prevent ambiguity.
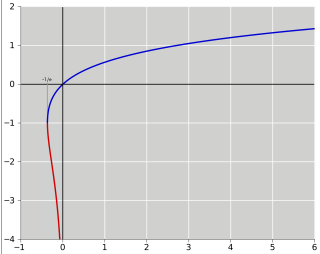
In mathematics, the Lambert W function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the inverse relation of the function f(w) = wew, where w is any complex number and ew is the exponential function.
In mathematics, a recurrence relation is an equation that recursively defines a sequence or multidimensional array of values, once one or more initial terms are given; each further term of the sequence or array is defined as a function of the preceding terms.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling of how a quantity such as heat diffuses through a given region.
In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:
In mathematics and its applications, classical Sturm–Liouville theory is the theory of real second-order linear ordinary differential equations of the form:
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.
In mathematics, the method of Frobenius, named after Ferdinand Georg Frobenius, is a way to find an infinite series solution for a second-order ordinary differential equation of the form
In mathematics, the Riemann series theorem, named after 19th-century German mathematician Bernhard Riemann, says that if an infinite series of real numbers is conditionally convergent, then its terms can be arranged in a permutation so that the new series converges to an arbitrary real number, or diverges.
In mathematics, an ordinary differential equation of the form

Lazarus Immanuel Fuchs was a Jewish-German mathematician who contributed important research in the field of linear differential equations. He was born in Moschin (Mosina) and died in Berlin, Germany. He was buried in Schöneberg in the St. Matthew's Cemetery. His grave in section H is preserved and listed as a grave of honour of the State of Berlin.
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for different classes of equations. One of the most important is based on the notion of distributions.
In mathematical logic, a formal calculation is a calculation which is systematic, but without a rigorous justification. This means that we are manipulating the symbols in an expression using a generic substitution, without proving that the necessary conditions hold. Essentially, we are interested in the form of an expression, and not necessarily its underlying meaning. This reasoning can either serve as positive evidence that some statement is true, when it is difficult or unnecessary to provide a proof, or as an inspiration for the creation of new definitions.
In mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.
In mathematics, an ordinary differential equation (ODE) is a differential equation containing one or more functions of one independent variable and the derivatives of those functions. The term ordinary is used in contrast with the term partial differential equation which may be with respect to more than one independent variable.














