Function field may refer to:
 | This disambiguation page lists mathematics articles associated with the same title. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
In mathematics, a field F is algebraically closed if every non-constant polynomial in F[x] has a root in F.
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical problems about these sets of zeros.
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
Linear algebra is the branch of mathematics concerning linear equations such as
Vector calculus, or vector analysis, is a branch of mathematics concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which includes vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields and fluid flow.
In mathematics, the term linear function refers to two distinct but related notions:
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and function fields. These properties, such as whether a ring admits unique factorization, the behavior of ideals, and the Galois groups of fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations.
In mathematics, particularly in algebraic geometry, complex analysis and algebraic number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions. Abelian varieties are at the same time among the most studied objects in algebraic geometry and indispensable tools for much research on other topics in algebraic geometry and number theory.
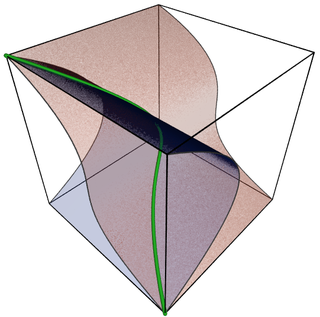
Algebraic varieties are the central objects of study in algebraic geometry. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. Modern definitions generalize this concept in several different ways, while attempting to preserve the geometric intuition behind the original definition.
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
In mathematics, an (algebraic) function field of n variables over the field k is a finitely generated field extension K/k which has transcendence degree n over k. Equivalently, an algebraic function field of n variables over k may be defined as a finite field extension of the field K=k(x1,...,xn) of rational functions in n variables over k.
Lists of mathematics topics cover a variety of topics related to mathematics. Some of these lists link to hundreds of articles; some link only to a few. The template to the right includes links to alphabetical lists of all mathematical articles. This article brings together the same content organized in a manner better suited for browsing. Lists cover aspects of basic and advanced mathematics, methodology, mathematical statements, integrals, general concepts, mathematical objects, integrals and reference tables. They also cover equations named after people, societies, mathematicians, journals and meta-lists.
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 or x**2 may be used in place of x2.
In mathematics, differential refers to infinitesimal differences or to the derivatives of functions. The term is used in various branches of mathematics such as calculus, differential geometry, algebraic geometry and algebraic topology.
Mathematics encompasses a growing variety and depth of subjects over history, and comprehension requires a system to categorize and organize the many subjects into more general areas of mathematics. A number of different classification schemes have arisen, and though they share some similarities, there are differences due in part to the different purposes they serve. In addition, as mathematics continues to be developed, these classification schemes must change as well to account for newly created areas or newly discovered links between different areas. Classification is made more difficult by some subjects, often the most active, which straddle the boundary between different areas.
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V. In classical algebraic geometry they are ratios of polynomials; in complex algebraic geometry these are meromorphic functions and their higher-dimensional analogues; in modern algebraic geometry they are elements of some quotient ring's field of fractions.
Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. It includes everything from elementary equation solving to the study of abstractions such as groups, rings, and fields. The more basic parts of algebra are called elementary algebra; the more abstract parts are called abstract algebra or modern algebra. Elementary algebra is generally considered to be essential for any study of mathematics, science, or engineering, as well as such applications as medicine and economics. Abstract algebra is a major area in advanced mathematics, studied primarily by professional mathematicians.
In mathematics, an algebraic number fieldF is a finite degree field extension of the field of rational numbers Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space over Q.
A two-dimensional conformal field theory is a quantum field theory on a Euclidean two-dimensional space, that is invariant under local conformal transformations.