 | This article needs additional citations for verification .(July 2018) |
In combinatorial game theory, a fuzzy game is a game which is incomparable with the zero game: it is not greater than 0, which would be a win for Left; nor less than 0 which would be a win for Right; nor equal to 0 which would be a win for the second player to move. It is therefore a first-player win. [1]
In combinatorial game theory, there are four types of game. If we denote players as Left and Right, and G be a game with some value, we have the following types of game:
1. Left win: G > 0
2. Right win: G < 0
3. Second player win: G = 0
4. First player win: G ║ 0 (G is fuzzy with 0)
Using standard Dedekind-section game notation, {L|R}, where L is the list of undominated moves for Left and R is the list of undominated moves for Right, a fuzzy game is a game where all moves in L are strictly non-negative, and all moves in R are strictly non-positive.
One example is the fuzzy game * = {0|0}, which is a first-player win, since whoever moves first can move to a second player win, namely the zero game. An example of a fuzzy game would be a normal game of Nim where only one heap remained where that heap includes more than one object.
Another example is the fuzzy game {1|-1}. Left could move to 1, which is a win for Left, while Right could move to -1, which is a win for Right; again this is a first-player win.
In Blue-Red-Green Hackenbush, if there is only a green edge touching the ground, it is a fuzzy game because the first player may take it and win (everything else disappears).
No fuzzy game can be a surreal number.
Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.
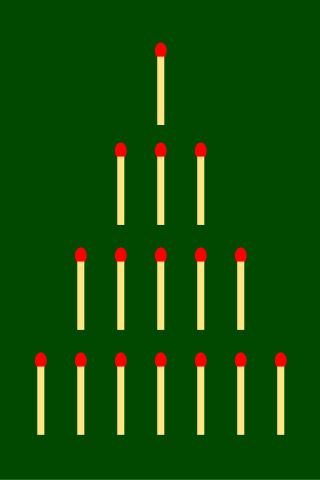
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps or piles. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap or pile. Depending on the version being played, the goal of the game is either to avoid taking the last object or to take the last object.
Zero-sum game is a mathematical representation in game theory and economic theory of a situation that involves two competing entities, where the result is an advantage for one side and an equivalent loss for the other. In other words, player one's gain is equivalent to player two's loss, with the result that the net improvement in benefit of the game is zero.
In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a one-heap game of nim, or to an infinite generalization of nim. It can therefore be represented as a natural number, the size of the heap in its equivalent game of nim, as an ordinal number in the infinite generalization, or alternatively as a nimber, the value of that one-heap game in an algebraic system whose addition operation combines multiple heaps to form a single equivalent heap in nim.
In game theory, the Nash equilibrium is the most commonly-used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy. The idea of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to his model of competition in an oligopoly.
In mathematics, the surreal number system is a totally ordered proper class containing not only the real numbers but also infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number. Research on the Go endgame by John Horton Conway led to the original definition and construction of surreal numbers. Conway's construction was introduced in Donald Knuth's 1974 book Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics and Found Total Happiness.
On Numbers and Games is a mathematics book by John Horton Conway first published in 1976. The book is written by a pre-eminent mathematician, and is directed at other mathematicians. The material is, however, developed in a playful and unpretentious manner and many chapters are accessible to non-mathematicians. Martin Gardner discussed the book at length, particularly Conway's construction of surreal numbers, in his Mathematical Games column in Scientific American in September 1976.
The sorites paradox is a paradox that results from vague predicates. A typical formulation involves a heap of sand, from which grains are removed individually. With the assumption that removing a single grain does not cause a heap to not be considered a heap anymore, the paradox is to consider what happens when the process is repeated enough times that only one grain remains: is it still a heap? If not, when did it change from a heap to a non-heap?
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field.
In combinatorial game theory, star, written as or , is the value given to the game where both players have only the option of moving to the zero game. Star may also be denoted as the surreal form {0|0}. This game is an unconditional first-player win.
In combinatorial game theory, the zero game is the game where neither player has any legal options. Therefore, under the normal play convention, the first player automatically loses, and it is a second-player win. The zero game has a Sprague–Grundy value of zero. The combinatorial notation of the zero game is: { | }.
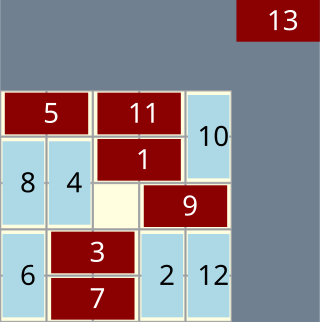
Domineering is a mathematical game that can be played on any collection of squares on a sheet of graph paper. For example, it can be played on a 6×6 square, a rectangle, an entirely irregular polyomino, or a combination of any number of such components. Two players have a collection of dominoes which they place on the grid in turn, covering up squares. One player places tiles vertically, while the other places them horizontally. As in most games in combinatorial game theory, the first player who cannot move loses.
In game theory, a move, action, or play is any one of the options which a player can choose in a setting where the optimal outcome depends not only on their own actions but on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship.
Game theory is the branch of mathematics in which games are studied: that is, models describing human behaviour. This is a glossary of some terms of the subject.
Hackenbush is a two-player game invented by mathematician John Horton Conway. It may be played on any configuration of colored line segments connected to one another by their endpoints and to a "ground" line.
In game theory, trembling hand perfect equilibrium is a type of refinement of a Nash equilibrium that was first proposed by Reinhard Selten. A trembling hand perfect equilibrium is an equilibrium that takes the possibility of off-the-equilibrium play into account by assuming that the players, through a "slip of the hand" or tremble, may choose unintended strategies, albeit with negligible probability.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.
The octal games are a class of two-player games that involve removing tokens from heaps of tokens. They have been studied in combinatorial game theory as a generalization of Nim, Kayles, and similar games.
The combinatorial game Toads and Frogs is a partisan game invented by Richard Guy. This mathematical game was used as an introductory game in the book Winning Ways for your Mathematical Plays.
In combinatorial game theory, a branch of mathematics studying two-player games of perfect information in extensive form, tiny and miny are operators that transform one game into another. When applied to a number they yield infinitesimal values.