The Gardner equation is an integrable nonlinear partial differential equation introduced by the mathematician Clifford Gardner in 1968 to generalize KdV equation and modified KdV equation. The Gardner equation has applications in hydrodynamics, plasma physics and quantum field theory [1]
where is an arbitrary real parameter.
The calculus of variations is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations.
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate the corresponding electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson who published it in 1823.
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
Linear elasticity is a mathematical model as to how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
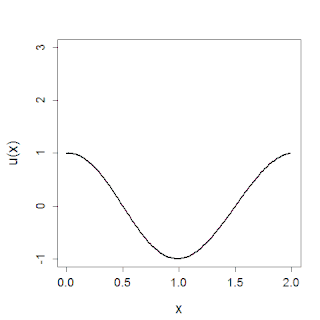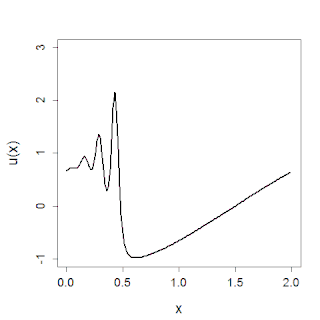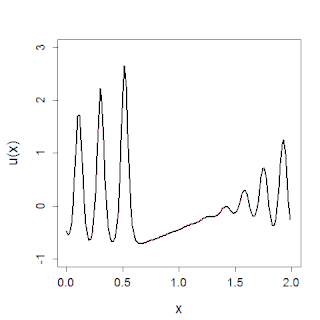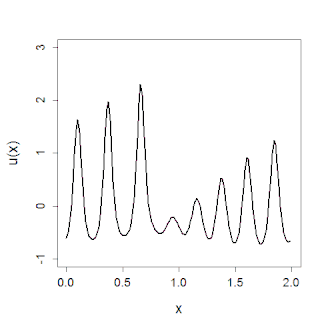
In mathematics, the Korteweg–De Vries (KdV) equation is a partial differential equation (PDE) which serves as a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an integrable PDE, exhibiting typical behaviors such as a large number of explicit solutions, in particular soliton solutions, and an infinite number of conserved quantities, despite the nonlinearity which typically renders PDEs intractable. The KdV can be solved by the inverse scattering method (ISM). In fact, Clifford Gardner, John M. Greene, Martin Kruskal and Robert Miura developed the classical inverse scattering method to solve the KdV equation.
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates (q, p) → that preserves the form of Hamilton's equations. This is sometimes known as form invariance. Although Hamilton's equations are preserved, it need not preserve the explicit form of the Hamiltonian itself. Canonical transformations are useful in their own right, and also form the basis for the Hamilton–Jacobi equations and Liouville's theorem.
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.
In mathematics, more specifically in dynamical systems, the method of averaging exploits systems containing time-scales separation: a fast oscillationversus a slow drift. It suggests that we perform an averaging over a given amount of time in order to iron out the fast oscillations and observe the qualitative behavior from the resulting dynamics. The approximated solution holds under finite time inversely proportional to the parameter denoting the slow time scale. It turns out to be a customary problem where there exists the trade off between how good is the approximated solution balanced by how much time it holds to be close to the original solution.
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
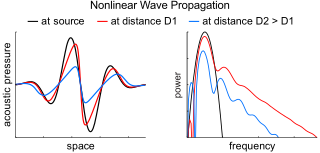
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.
In mathematics and physics, multiple-scale analysis comprises techniques used to construct uniformly valid approximations to the solutions of perturbation problems, both for small as well as large values of the independent variables. This is done by introducing fast-scale and slow-scale variables for an independent variable, and subsequently treating these variables, fast and slow, as if they are independent. In the solution process of the perturbation problem thereafter, the resulting additional freedom – introduced by the new independent variables – is used to remove (unwanted) secular terms. The latter puts constraints on the approximate solution, which are called solvability conditions.
In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory rigorously justifies the modelling. For example, some global and regional models of the atmosphere or oceans resolve the so-called quasi-geostrophic flow dynamics on the slow manifold of the atmosphere/oceanic dynamics, and is thus crucial to forecasting with a climate model.
The Tzitzeica equation is a nonlinear partial differential equation devised by Gheorghe Țițeica in 1907 in the study of differential geometry, describing surfaces of constant affine curvature. The Tzitzeica equation has also been used in nonlinear physics, being an integrable 1+1 dimensional Lorentz invariant system.
Unnormalized KdV equation is a nonlinear partial differential equation
The Dodd–Bullough–Mikhailov equation is a nonlinear partial differential equation introduced by Roger Dodd, Robin Bullough, and Alexander Mikhailov.
The Broer–Kaup equations are a set of two coupled nonlinear partial differential equations:
The Chafee–Infante equation is a nonlinear partial differential equation introduced by Nathaniel Chafee and Ettore Infante.
The Estevez–Mansfield–Clarkson equation is a nonlinear partial differential equation introduced by Pilar Estevez, Elizabeth Mansfield, and Peter Clarkson.
The Hirota–Satsuma equation is a set of three coupled nonlinear partial differential equations:
 | This article about theoretical physics is a stub. You can help Wikipedia by expanding it. |
