In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:
In optics, polarized light can be described using the Jones calculus, discovered by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices. When light crosses an optical element the resulting polarization of the emerging light is found by taking the product of the Jones matrix of the optical element and the Jones vector of the incident light. Note that Jones calculus is only applicable to light that is already fully polarized. Light which is randomly polarized, partially polarized, or incoherent must be treated using Mueller calculus.

A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth to find geographical direction automatically. A gyrocompass makes use of one of the seven fundamental ways to determine the heading of a vehicle. A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect. Gyrocompasses are widely used for navigation on ships, because they have two significant advantages over magnetic compasses:

In physics, angular velocity, also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates around an axis of rotation and how fast the axis itself changes direction.
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.

A tautochrone curve or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid.

A sine wave, sinusoidal wave, or sinusoid is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is simple harmonic motion; as rotation, it corresponds to uniform circular motion. Sine waves occur often in physics, including wind waves, sound waves, and light waves. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies.
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with functions of other variables. The intent is that when expressed in new variables, the problem may become simpler, or equivalent to a better understood problem.
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.

In geometry, a trochoid is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle as it rolls along a straight line. If the point is on the circle, the trochoid is called common ; if the point is inside the circle, the trochoid is curtate; and if the point is outside the circle, the trochoid is prolate. The word "trochoid" was coined by Gilles de Roberval.

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.

In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where, as a parameter changes, a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis as a parameter crosses a threshold value. Under reasonably generic assumptions about the dynamical system, the fixed point becomes a small-amplitude limit cycle as the parameter changes.
In mathematics, more specifically in dynamical systems, the method of averaging exploits systems containing time-scales separation: a fast oscillationversus a slow drift. It suggests that we perform an averaging over a given amount of time in order to iron out the fast oscillations and observe the qualitative behavior from the resulting dynamics. The approximated solution holds under finite time inversely proportional to the parameter denoting the slow time scale. It turns out to be a customary problem where there exists the trade off between how good is the approximated solution balanced by how much time it holds to be close to the original solution.
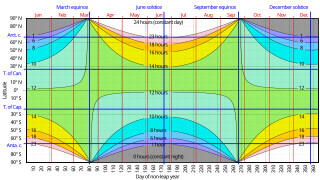
The sunrise equation or sunset equation can be used to derive the time of sunrise or sunset for any solar declination and latitude in terms of local solar time when sunrise and sunset actually occur.
In electronic music, waveshaping is a type of distortion synthesis in which complex spectra are produced from simple tones by altering the shape of the waveforms.
An electric dipole transition is the dominant effect of an interaction of an electron in an atom with the electromagnetic field.
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is adapted to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented.
In physics, and especially scattering theory, the momentum-transfer cross section is an effective scattering cross section useful for describing the average momentum transferred from a particle when it collides with a target. Essentially, it contains all the information about a scattering process necessary for calculating average momentum transfers but ignores other details about the scattering angle.
Blade element momentum theory is a theory that combines both blade element theory and momentum theory. It is used to calculate the local forces on a propeller or wind-turbine blade. Blade element theory is combined with momentum theory to alleviate some of the difficulties in calculating the induced velocities at the rotor.

















