Generalized geography

Last updated

In computational complexity theory, generalized geography is a well-known PSPACE-complete problem.

Contents

Introduction

Geography is a children's game, which is good for a long car trip, where players take turns naming cities from anywhere in the world. Each city chosen must begin with the same letter that ended the previous city name. Repetition is not allowed. The game begins with an arbitrary starting city and ends when a player loses because he or she is unable to continue.

Graph model

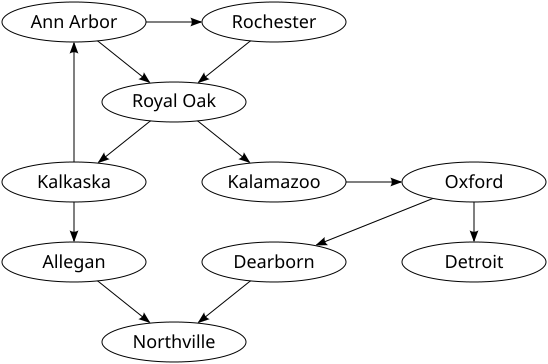
To visualize the game, a directed graph can be constructed whose nodes are each cities of the world. An arrow is added from node N1 to node N2 if and only if the city labeling N2 starts with the letter that ending the name of the city labeling node N1. In other words, we draw an arrow from one city to another if the first can lead to the second according to the game rules. Each alternate edge in the directed graph corresponds to each player (for a two player game). The first player unable to extend the path loses. An illustration of the game (containing some cities in Michigan) is shown in the figure below.

Generalized geography 1.svg

In a generalized geography (GG) game, we replace the graph of city names with an arbitrary directed graph. The following graph is an example of a generalized geography game.

Generalized geography 2.png

Playing the game

We define P1 as the player moving first and P2 as the player moving second and name the nodes N1 to Nn. In the above figure, P1 has a winning strategy as follows: N1 points only to nodes N2 and N3. Thus P1's first move must be one of these two choices. P1 chooses N2 (if P1 chooses N3, then P2 will choose N9 as that is the only option and P1 will lose). Next P2 chooses N4 because it is the only remaining choice. P1 now chooses N5 and P2 subsequently chooses N3 or N7. Regardless of P2's choice, P1 chooses N9 and P2 has no remaining choices and loses the game.

Computational complexity

The problem of determining which player has a winning strategy in a generalized geography game is PSPACE-complete.

Generalized geography is in PSPACE

Let GG = { <G, b> | P1 has a winning strategy for the generalized geography game played on graph G starting at node b }; to show that GG ∈ PSPACE, we present a polynomial-space recursive algorithm determining which player has a winning strategy. Given an instance of GG, <G, nstart> where G is a directed graph and nstart is the designated start node, the algorithm M proceeds as follows:

On M(<G, nstart>):

  1. Measure the out-degree of node nstart. If this degree is 0, then return reject, because there are no moves available for player one.
  2. Construct a list of all nodes reachable from nstart by one edge: n1, n2, ..., ni.
  3. Remove nstart and all edges connected to it from G to form G1.
  4. For each node nj in the list n1, ..., ni, call M(<G1, nj>).
  5. If all of these calls return accept, then no matter which decision P1 makes, P2 has a strategy to win, so return reject. Otherwise (if one of the calls returns reject) P1 has a choice that will deny any successful strategies for P2, so return accept.

The algorithm M clearly decides GG. It is in PSPACE because the only non-obvious polynomial workspace consumed is in the recursion stack. The space consumed by the recursion stack is polynomial because each level of recursion adds a single node to the stack, and there are at most n levels, where n is the number of nodes in G. This is essentially equivalent to a depth-first search.

Generalized geography is PSPACE-hard

The following proof is due to David Lichtenstein and Michael Sipser. [1]

To establish the PSPACE-hardness of GG, we can reduce the FORMULA-GAME problem (which is known to be PSPACE-hard) to GG in polynomial time (P). In brief, an instance of the FORMULA-GAME problem consists of a quantified Boolean formula φ = ∃x1 ∀x2 ∃x3 ...Qxk(ψ) where Q is either ∃ or ∀. The game is played by two players, Pa and Pe, who alternate choosing values for successive xi. Pe wins the game if the formula ψ ends up true, and Pa wins if ψ ends up false. The formula ψ is assumed to be in conjunctive normal form.

In this proof, we assume that the quantifier list starts and ends with the existential qualifier, ∃, for simplicity. Note that any expression can be converted to this form by adding dummy variables that do not appear in ψ.

Generalized geography 3.png

By constructing a graph G like the one shown above, we will show any instance of FORMULA-GAME can be reduced to an instance of Generalized Geography, where the optimal strategy for P1 is equivalent to that of Pe, and the optimal strategy for P2 is equivalent to that of Pa.

The left vertical chain of nodes is designed to mimic the procedure of choosing values for variables in FORMULA-GAME. Each diamond structure corresponds to a quantified variable. Players take turns deciding paths at each branching node. Because we assumed the first quantifier would be existential, P1 goes first, selecting the left node if x1 is true and the right node if x1 is false. Each player must then take forced turns, and then P2 chooses a value for x2. These alternating assignments continue down the left side. After both players pass through all the diamonds, it is again P1 's turn, because we assumed that the last quantifier is existential. P1 has no choice but to follow the path to the right side of the graph. Then it is P2 's turn to make a move.

When the play gets to the right side of the graph, it is similar to the end of play in the formula game. Recall that in the formula game, Pe wins if ψ is true, while Pa wins if ψ is false. The right side of the graph guarantees that P1 wins if and only if Pe wins, and that P2 wins if and only if Pa wins.

First we show that P2 always wins when Pa wins. If Pa wins, ψ is false. If ψ is false, there exists an unsatisfying clause. P2 will choose an unsatisfying clause to win. Then when it is P1's turn he must choose a literal in that clause chosen by P2. Since all the literals in the clause are false, they do not connect to previously visited nodes in the left vertical chain. This allows P2 to follow the connection to the corresponding node in a diamond of the left chain and select it. However, P1 is now unable to select any adjacent nodes and loses.

Now we show that P1 always wins when Pe wins. If Pe wins, ψ is true. If ψ is true, every clause in the right side of the graph contains a true literal. P2 can choose any clause. Then P1 chooses the literal that is true. And because it is true, its adjacent node in the left vertical node has already been selected, so P2 has no moves to make and loses.

Planar generalized geography is PSPACE-complete

Generalized geography is PSPACE-complete, even when played on planar graphs. The following proof is from theorem 3 of. [1]

Since planar GG is a special case of GG, and GG is in PSPACE, so planar GG is in PSPACE. It remains to show that planar GG is PSPACE-hard. This can be proved by showing how to convert an arbitrary graph into a planar graph, such that a game of GG played on this graph will have the same outcome as on the original graph.

In order to do that, it's only necessary to eliminate all the edge crossings of the original graph. We draw the graph such that no three edges intersect at a point, and no pair of crossing edges can both be used in the same game. This is not possible in general, but is always possible for the graph constructed from a FORMULA-GAME instance; for example we could have only the edges from clause vertices involved in crossings. Now we replace each crossing with this construction:

Generalized geography - transformation to a planar graph.svg

The result is a planar graph, and the same player can force a win as in the original graph: if a player chooses to move "up" from V in the transformed game, then both players must continuing moving "up" to W or lose immediately. So moving "up" from V in the transformed game simulates the move V→W in the original game. If V→W is a winning move, then moving "up" from V in the transformed game is also a winning move, and vice versa.

Thus, the game of GG played on the transformed graph will have the same outcome as on the original graph. This transformation takes time that is a constant multiple to the number of edge intersections in the original graph, thus it takes polynomial time.

Thus planar GG is PSPACE-complete.

Planar bipartite graph with maximum degree 3

GG played on planar bipartite graphs with maximum degree 3 is still PSPACE-complete, by replacing the vertices of degree higher than 3 with a chain of vertices with degree at most 3. Proof is in. [1] and uses the following construction:

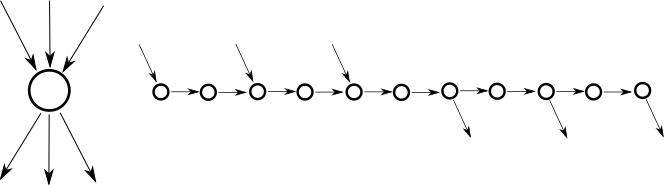
Generalized geography 3-planar transformation.svg

If one player uses any of the entrances to this construction, the other player chooses which exit will be used. Also the construction can only be traversed once, because the central vertex is always visited. Hence this construction is equivalent to the original vertex.

Edge geography

A variant of GG is called edge geography, where after each move, the edge that the player went through is erased. This is in contrast to the original GG, where after each move, the vertex that the player used to be on is erased. In this view, the original GG can be called Vertex Geography.

Edge geography is PSPACE-complete. This can be proved used the same construction that was used for vertex geography. [2]

Undirected geography

One may also consider playing either Geography game on an undirected graph (that is, the edges can be traversed in both directions). Fraenkel, Scheinerman, and Ullman [3] show that undirected vertex geography can be solved in polynomial time, whereas undirected edge geography is PSPACE-complete, even for planar graphs with maximum degree 3. If the graph is bipartite, then Undirected Edge Geography is solvable in polynomial time.

Consequences

Given that GG is PSPACE-complete, no polynomial time algorithm exists for optimal play in GG unless P = PSPACE. However, it may not be as easy to prove the complexity of other games because certain games (such as chess) contain a finite number of game positions — making it hard (or impossible) to formulate a mapping to a PSPACE-complete problem. In spite of this, the complexity of certain games can still be analyzed by generalization (e.g., to an n × n board). See the references for a proof for generalized Go, as a corollary of the proof of the completeness of GG.

Related Research Articles

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

Tree (graph theory) Undirected, connected and acyclic graph

In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by at most one path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees.

Hamiltonian path Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a Hamiltonian path that is a cycle. Determining whether such paths and cycles exist in graphs is the Hamiltonian path problem, which is NP-complete.

In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its even-degree subgraphs.

The Shannon switching game is a connection game for two players, invented by American mathematician and electrical engineer Claude Shannon, the "father of information theory" some time before 1951. Two players take turns coloring the edges of an arbitrary graph. One player has the goal of connecting two distinguished vertices by a path of edges of their color. The other player aims to prevent this by using their color instead. The game is commonly played on a rectangular grid; this special case of the game was independently invented by American mathematician David Gale in the late 1950s and is known as Gale or Bridg-It.

Graph coloring Assignment of colors to elements of a graph subject to certain constraints.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

Spanning tree

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.

Circuit rank

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula

Dual graph

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In computer science, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.

In graph theory, a nowhere-zero flow or NZ flow is a network flow that is nowhere zero. It is intimately connected to coloring planar graphs.

Go and mathematics

The game of Go is one of the most popular games in the world. As a result of its elegant and simple rules, the game has long been an inspiration for mathematical research. Shen Kuo, a Chinese scholar in 11th century, estimated that the number of possible board positions is around 10172 in The Dream Pool Essays. In more recent years, research of the game by John H. Conway led to the invention of the surreal numbers and contributed to development of combinatorial game theory (with Go Infinitesimals being a specific example of its use in Go).

Pseudoforest

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.

In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified, using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false. If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT.

In graph theory, the tree-depth of a connected undirected graph G is a numerical invariant of G, the minimum height of a Trémaux tree for a supergraph of G. This invariant and its close relatives have gone under many different names in the literature, including vertex ranking number, ordered chromatic number, and minimum elimination tree height; it is also closely related to the cycle rank of directed graphs and the star height of regular languages. Intuitively, where the treewidth graph width parameter measures how far a graph is from being a tree, this parameter measures how far a graph is from being a star.

Pancyclic graph

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

Well-covered graph

In graph theory, a well-covered graph is an undirected graph in which every minimal vertex cover has the same size as every other minimal vertex cover. Equivalently, these are the graphs in which every maximal independent set has the same size. Well-covered graphs were defined and first studied by Plummer (1970).

In theoretical computer science, nondeterministic constraint logic is a combinatorial system in which an orientation is given to the edges of a weighted undirected graph, subject to certain constraints. One can change this orientation by steps in which a single edge is reversed, subject to the same constraints. The constraint logic problem and its variants have been proven to be PSPACE-complete to determine whether there exists a sequence of moves that reverses a specified edge and are very useful to show various games and puzzles are PSPACE-hard or PSPACE-complete.

References

  1. 1 2 3 Lichtenstein, David; Sipser, Michael (April 1980). "Go Is Polynomial-Space Hard" (PDF). Journal of the ACM. 27 (2): 393–401. doi:10.1145/322186.322201.
  2. ↑ Schaefer, Thomas J. (1978). "On the complexity of some two-person perfect-information games". Journal of Computer and System Sciences. 16 (2): 185–225. doi: 10.1016/0022-0000(78)90045-4 .
  3. ↑ Fraenkel, Aviezri; Scheinerman, Edward; Ullman, Daniel (1993). "Undirected edge geography". Theoretical Computer Science. 112 (2): 371–381. doi: 10.1016/0304-3975(93)90026-p .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.