In number theory, Euler's conjecture is a disproved conjecture related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers n and k greater than 1, if the sum of n many kth powers of positive integers is itself a kth power, then n is greater than or equal to k:

In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers. Due to its subtlety, it has many formulations, but the most standard statement is:

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as for , and its analytic continuation elsewhere.

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 32. The smallest positive square-free numbers are
In mathematics, a transcendental number is a real or complex number that is not algebraic – that is, not the root of a non-zero polynomial of finite degree with integer coefficients. The best-known transcendental numbers are π and e. The quality of a number being transcendental is called transcendence.
19 (nineteen) is the natural number following 18 and preceding 20. It is a prime number.

Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as a sum of four non-negative integer squares. That is, the squares form an additive basis of order four. where the four numbers are integers. For illustration, 3, 31, and 310 in several ways, can be represented as the sum of four squares as follows:
A powerful number is a positive integer m such that for every prime number p dividing m, p2 also divides m. Equivalently, a powerful number is the product of a square and a cube, that is, a number m of the form m = a2b3, where a and b are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers powerful.
1729 is the natural number following 1728 and preceding 1730. It is notably the first nontrivial taxicab number.

In mathematics, the nth taxicab number, typically denoted Ta(n) or Taxicab(n), is defined as the smallest integer that can be expressed as a sum of two positive integer cubes in n distinct ways. The most famous taxicab number is 1729 = Ta(2) = 13 + 123 = 93 + 103, also known as the Hardy-Ramanujan number.
In mathematics, a harshad number in a given number base is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers in base n are also known as n-harshad numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The term "Niven number" arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977.
In number theory, the n-th cabtaxi number, typically denoted Cabtaxi(n), is defined as the smallest positive integer that can be written as the sum of two positive or negative or 0 cubes in n ways. Such numbers exist for all n, which follows from the analogous result for taxicab numbers.
The Beal conjecture is the following conjecture in number theory:
1728 is the natural number following 1727 and preceding 1729. It is a dozen gross, or one great gross. It is also the number of cubic inches in a cubic foot.
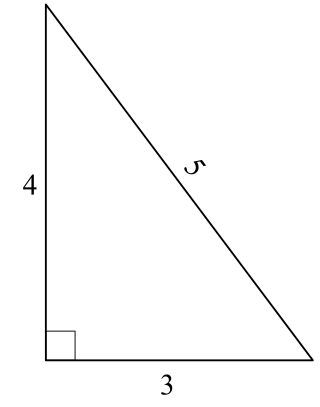
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number.
In mathematics and statistics, sums of powers occur in a number of contexts:
The Erdős–Turán conjecture is an old unsolved problem in additive number theory posed by Paul Erdős and Pál Turán in 1941.
The Lander, Parkin, and Selfridge conjecture concerns the integer solutions of equations which contain sums of like powers. The equations are generalisations of those considered in Fermat's Last Theorem. The conjecture is that if the sum of some k-th powers equals the sum of some other k-th powers, then the total number of terms in both sums combined must be at least k.
In additive number theory, an area of mathematics, the Erdős–Tetali theorem is an existence theorem concerning economical additive bases of every order. More specifically, it states that for every fixed integer , there exists a subset of the natural numbers satisfying

In mathematics, the sum of two cubes is a cubed number added to another cubed number.









