A geodesic is a curve representing in some sense the shortest path between two points on a surface.
 | Look up geodesic in Wiktionary, the free dictionary. |
Geodesic may also refer to:
 | This disambiguation page lists articles associated with the title Geodesic. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
A great circle, also known as an orthodrome, of a sphere is the intersection of the sphere and a plane that passes through the center point of the sphere. A great circle is the largest circle that can be drawn on any given sphere. Any diameter of any great circle coincides with a diameter of the sphere, and therefore all great circles have the same center and circumference as each other. This special case of a circle of a sphere is in opposition to a small circle, that is, the intersection of the sphere and a plane that does not pass through the center. Every circle in Euclidean 3-space is a great circle of exactly one sphere.
A geodesic dome is a hemispherical thin-shell structure (lattice-shell) based on a geodesic polyhedron. The triangular elements of the dome are structurally rigid and distribute the structural stress throughout the structure, making geodesic domes able to withstand very heavy loads for their size.
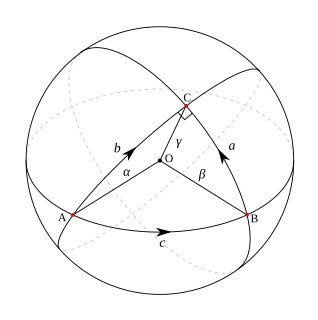
In geometry, a geodesic is commonly a curve representing in some sense the shortest path between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line" to a more general setting.
The world line of an object is the path that object traces in 4-dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics.
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection, then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the connection.
The Penrose–Hawking singularity theorems are a set of results in general relativity that attempt to answer the question of when gravitation produces singularities. Penrose would go on to win the 2020 Nobel Prize in Physics "for the discovery that black hole formation is a robust prediction of the general theory of relativity", which he shared with Reinhard Genzel and Andrea Ghez.
In Riemannian geometry, the geodesic curvature of a curve measures how far the curve is from being a geodesic. For example, for 1D curves on a 2D surface embedded in 3D space, it is the curvature of the curve projected onto the surface's tangent plane. More generally, in a given manifold , the geodesic curvature is just the usual curvature of . However, when the curve is restricted to lie on a submanifold of , geodesic curvature refers to the curvature of in and it is different in general from the curvature of in the ambient manifold . The (ambient) curvature of depends on two factors: the curvature of the submanifold in the direction of , which depends only on the direction of the curve, and the curvature of seen in , which is a second order quantity. The relation between these is . In particular geodesics on have zero geodesic curvature, so that , which explains why they appear to be curved in ambient space whenever the submanifold is.
A geodetic airframe is a type of construction for the airframes of aircraft developed by British aeronautical engineer Barnes Wallis in the 1930s. Earlier, it was used by Prof. Schütte for the Schütte Lanz Airship LS 1 in 1909. It makes use of a space frame formed from a spirally crossing basket-weave of load-bearing members. The principle is that two geodesic arcs can be drawn to intersect on a curving surface in a manner that the torsional load on each cancels out that on the other.
General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.
In general relativity, a congruence is the set of integral curves of a vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime. Often this manifold will be taken to be an exact or approximate solution to the Einstein field equation.
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves. In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting".
In mathematics, the geodesic equations are second-order non-linear differential equations, and are commonly presented in the form of Euler–Lagrange equations of motion. However, they can also be presented as a set of coupled first-order equations, in the form of Hamilton's equations. This latter formulation is developed in this article.
The mathematics of general relativity is complex. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.
A geodesic grid is a spatial grid based on a geodesic polyhedron or Goldberg polyhedron.
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold is a geodesic that returns to its starting point with the same tangent direction. It may be formalized as the projection of a closed orbit of the geodesic flow on the tangent space of the manifold.
The study of geodesics on an ellipsoid arose in connection with geodesy specifically with the solution of triangulation networks. The figure of the Earth is well approximated by an oblate ellipsoid, a slightly flattened sphere. A geodesic is the shortest path between two points on a curved surface, analogous to a straight line on a plane surface. The solution of a triangulation network on an ellipsoid is therefore a set of exercises in spheroidal trigonometry.
In differential geometry the theorem of the three geodesics states that every Riemannian manifold with the topology of a sphere has at least three closed geodesics that form simple closed curves. The result can also be extended to quasigeodesics on a convex polyhedron.