Gould's sequence

Last updated
Pascal's triangle, rows 0 through 7. The number of odd integers in row i is the i-th number in Gould's sequence. Pascal triangle small.png
Pascal's triangle, rows 0 through 7. The number of odd integers in row i is the i-th number in Gould's sequence.
The self-similar sawtooth shape of Gould's sequence Gould sawtooth.svg
The self-similar sawtooth shape of Gould's sequence

Gould's sequence is an integer sequence named after Henry W. Gould that counts how many odd numbers are in each row of Pascal's triangle. It consists only of powers of two, and begins: [1] [2]

Contents

1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, ... (sequence A001316 in the OEIS )

For instance, the sixth number in the sequence is 4, because there are four odd numbers in the sixth row of Pascal's triangle (the four bold numbers in the sequence 1, 5, 10, 10, 5, 1).

Additional interpretations

The nth value in the sequence (starting from n = 0) gives the highest power of 2 that divides the central binomial coefficient , and it gives the numerator of (expressed as a fraction in lowest terms). [1]

Sierpinski triangle generated by Rule 90, or by marking the positions of odd numbers in Pascal's triangle. Gould's sequence counts the number of live cells in each row of this pattern. PascalungeradeDreiecke.svg
Sierpinski triangle generated by Rule 90, or by marking the positions of odd numbers in Pascal's triangle. Gould's sequence counts the number of live cells in each row of this pattern.

Gould's sequence also gives the number of live cells in the nth generation of the Rule 90 cellular automaton starting from a single live cell. [1] [3] It has a characteristic growing sawtooth shape that can be used to recognize physical processes that behave similarly to Rule 90. [4]

The binary logarithms (exponents in the powers of two) of Gould's sequence themselves form an integer sequence,

0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, ... (sequence A000120 in the OEIS )

in which the nth value gives the number of nonzero bits in the binary representation of the number n, sometimes written in mathematical notation as . [1] [2] Equivalently, the nth value in Gould's sequence is

Taking the sequence of exponents modulo two gives the Thue–Morse sequence. [5]

The partial sums of Gould's sequence,

0, 1, 3, 5, 9, 11, 15, 19, 27, 29, 33, 37, 45, ... (sequence A006046 in the OEIS )

count all odd numbers in the first n rows of Pascal's triangle. These numbers grow proportionally to , but with a constant of proportionality that oscillates between 0.812556... and 1, periodically as a function of log n. [6] [7]

Recursive construction and self-similarity

The first 2i values in Gould's sequence may be constructed by recursively constructing the first 2i− 1 values, and then concatenating the doubles of the first 2i− 1 values. For instance, concatenating the first four values 1, 2, 2, 4 with their doubles 2, 4, 4, 8 produces the first eight values. Because of this doubling construction, the first occurrence of each power of two 2i in this sequence is at position 2i− 1. [1]

Gould's sequence, the sequence of its exponents, and the Thue–Morse sequence are all self-similar: they have the property that the subsequence of values at even positions in the whole sequence equals the original sequence, a property they also share with some other sequences such as Stern's diatomic sequence. [3] [8] [9] In Gould's sequence, the values at odd positions are double their predecessors, while in the sequence of exponents, the values at odd positions are one plus their predecessors.

History

The sequence is named after Henry W. Gould, who studied it in the early 1960s. However, the fact that these numbers are powers of two, with the exponent of the nth number equal to the number of ones in the binary representation of n, was already known to J. W. L. Glaisher in 1899. [10] [11]

Proving that the numbers in Gould's sequence are powers of two was given as a problem in the 1956 William Lowell Putnam Mathematical Competition. [12]

Related Research Articles

In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial:

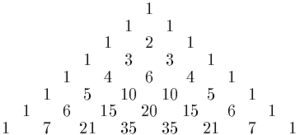
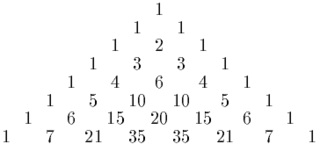
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients arising in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.

2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.

<span class="mw-page-title-main">Power of two</span> Two raised to an integer power

A power of two is a number of the form 2n where n is an integer, that is, the result of exponentiation with number two as the base and integer n as the exponent.

<span class="mw-page-title-main">Square pyramidal number</span> Number of stacked spheres in a pyramid

In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.

126 is the natural number following 125 and preceding 127.

<span class="mw-page-title-main">Pascal's pyramid</span>

In mathematics, Pascal's pyramid is a three-dimensional arrangement of the trinomial numbers, which are the coefficients of the trinomial expansion and the trinomial distribution. Pascal's pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial numbers and relates to the binomial expansion and the binomial distribution. The binomial and trinomial numbers, coefficients, expansions, and distributions are subsets of the multinomial constructs with the same names.

<span class="mw-page-title-main">Pentatope number</span> Number in the 5th cell of any row of Pascals triangle

In number theory, a pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1, either from left to right or from right to left. It is named because it represents the number of 3-dimensional unit spheres which can be packed into a pentatope of increasing side lengths.

In mathematics, Wolstenholme's theorem states that for a prime number , the congruence

1023 is the natural number following 1022 and preceding 1024.

<span class="mw-page-title-main">Central binomial coefficient</span> Sequence of numbers ((2n) choose (n))

In mathematics the nth central binomial coefficient is the particular binomial coefficient

In number theory, an odious number is a positive integer that has an odd number of 1s in its binary expansion. Non-negative integers that are not odious are called evil numbers.

Lozanić's triangle is a triangular array of binomial coefficients in a manner very similar to that of Pascal's triangle. It is named after the Serbian chemist Sima Lozanić, who researched it in his investigation into the symmetries exhibited by rows of paraffins.

Singmaster's conjecture is a conjecture in combinatorial number theory, named after the British mathematician David Singmaster who proposed it in 1971. It says that there is a finite upper bound on the multiplicities of entries in Pascal's triangle. It is clear that the only number that appears infinitely many times in Pascal's triangle is 1, because any other number x can appear only within the first x + 1 rows of the triangle.

1728 is the natural number following 1727 and preceding 1729. It is a dozen gross, or one great gross. It is also the number of cubic inches in a cubic foot.

288 is the natural number following 287 and preceding 289. Because 288 = 2 · 12 · 12, it may also be called "two gross" or "two dozen dozen".

In combinatorial mathematics, the Lobb numberLm,n counts the number of ways that n + m open parentheses and n − m close parentheses can be arranged to form the start of a valid sequence of balanced parentheses.

<span class="mw-page-title-main">Bell triangle</span>

In mathematics, the Bell triangle is a triangle of numbers analogous to Pascal's triangle, whose values count partitions of a set in which a given element is the largest singleton. It is named for its close connection to the Bell numbers, which may be found on both sides of the triangle, and which are in turn named after Eric Temple Bell. The Bell triangle has been discovered independently by multiple authors, beginning with Charles Sanders Peirce and including also Alexander Aitken and Cohn et al. (1962), and for that reason has also been called Aitken's array or the Peirce triangle.

<span class="mw-page-title-main">Bernoulli's triangle</span> Array of partial sums of the binomial coefficients

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by:

In mathematics, the fibbinary numbers are the numbers whose binary representation does not contain two consecutive ones. That is, they are sums of distinct and non-consecutive powers of two.

References

  1. 1 2 3 4 5 Sloane, N. J. A. (ed.). "SequenceA001316(Gould's sequence)". The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.
  2. 1 2 Pólya, George; Tarjan, Robert E.; Woods, Donald R. (2009), Notes on Introductory Combinatorics, Progress in Computer Science and Applied Logic, vol. 4, Springer, p. 21, ISBN   9780817649531 .
  3. 1 2 Wolfram, Stephen (1984), "Geometry of binomial coefficients", American Mathematical Monthly , 91 (9): 566–571, doi:10.2307/2323743, JSTOR   2323743, MR   0764797 .
  4. ↑ Claussen, Jens Christian; Nagler, Jan; Schuster, Heinz Georg (2004), "Sierpinski signal generates 1/f α spectra", Physical Review E, 70 (3): 032101, arXiv: cond-mat/0308277 , Bibcode:2004PhRvE..70c2101C, doi:10.1103/PhysRevE.70.032101, PMID   15524560, S2CID   39929111 .
  5. ↑ Northshield, Sam (2010), "Sums across Pascal's triangle mod 2", Congressus Numerantium, 200: 35–52, MR   2597704, archived from the original on 2015-09-10, retrieved 2016-09-10.
  6. ↑ Harborth, Heiko (1976), "Number of odd binomial coefficients", Proceedings of the American Mathematical Society , 62 (1): 19–22, doi: 10.2307/2041936 , JSTOR   2041936, MR   0429714 .
  7. ↑ Larcher, G. (1996), "On the number of odd binomial coefficients", Acta Mathematica Hungarica , 71 (3): 183–203, doi:10.1007/BF00052108, MR   1397551, S2CID   121576268 .
  8. ↑ Gilleland, Michael, Some Self-Similar Integer Sequences, OEIS, retrieved 2016-09-10.
  9. ↑ Schroeder, Manfred (1996), "Fractals in Music", in Pickover, Clifford A. (ed.), Fractal Horizons, New York: St. Martin's Press, pp. 207–223. As cited by Gilleland.
  10. ↑ Granville, Andrew (1992), "Zaphod Beeblebrox's brain and the fifty-ninth row of Pascal's triangle", American Mathematical Monthly , 99 (4): 318–331, doi:10.2307/2324898, JSTOR   2324898, MR   1157222 .
  11. ↑ Glaisher, J. W. L. (1899), "On the residue of a binomial-theorem coefficient with respect to a prime modulus", The Quarterly Journal of Pure and Applied Mathematics , 30: 150–156. See in particular the final paragraph of p. 156.
  12. ↑ Gleason, Andrew M.; Greenwood, R. E.; Kelly, Leroy Milton, eds. (1980), The William Lowell Putnam Mathematical Competition: Problems and Solutions: 1938–1964, Mathematical Association of America, p. 46, ISBN   9780883854624 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.