
A rocket is a spacecraft, aircraft, vehicle or projectile that obtains thrust from a rocket engine. Rocket engine exhaust is formed entirely from propellant carried within the rocket. Rocket engines work by action and reaction and push rockets forward simply by expelling their exhaust in the opposite direction at high speed, and can therefore work in the vacuum of space.

Spacecraft propulsion is any method used to accelerate spacecraft and artificial satellites. In-space propulsion exclusively deals with propulsion systems used in the vacuum of space and should not be confused with space launch or atmospheric entry.

A mass driver or electromagnetic catapult is a proposed method of non-rocket spacelaunch which would use a linear motor to accelerate and catapult payloads up to high speeds. Existing and contemplated mass drivers use coils of wire energized by electricity to make electromagnets, though a rotary mass driver has also been proposed. Sequential firing of a row of electromagnets accelerates the payload along a path. After leaving the path, the payload continues to move due to momentum.

In physics, escape velocity or escape speed is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a primary body, thus reaching an infinite distance from it. It is typically stated as an ideal speed, ignoring atmospheric friction. Although the term "escape velocity" is common, it is more accurately described as a speed than a velocity because it is independent of direction; the escape speed increases with the mass of the primary body and decreases with the distance from the primary body. The escape speed thus depends on how far the object has already traveled, and its calculation at a given distance takes into account the fact that without new acceleration it will slow down as it travels—due to the massive body's gravity—but it will never quite slow to a stop.

In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense.
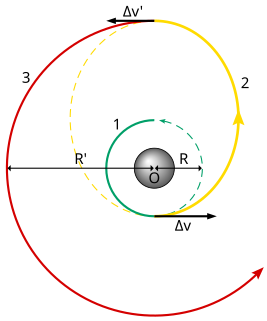
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different radii around a central body in the same plane. The Hohmann transfer often uses the lowest possible amount of propellant in traveling between these orbits, but bi-elliptic transfers can use less in some cases.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
Delta-v, symbolized as ∆v and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launching from or landing on a planet or moon, or an in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle.

The gravitational force equivalent, or, more commonly, g-force, is a measurement of the type of force per unit mass – typically acceleration – that causes a perception of weight, with a g-force of 1 g equal to the conventional value of gravitational acceleration on Earth, g, of about 9.8 m/s2. Since g-forces indirectly produce weight, any g-force can be described as a "weight per unit mass". When the g-force is produced by the surface of one object being pushed by the surface of another object, the reaction force to this push produces an equal and opposite weight for every unit of an object's mass. The types of forces involved are transmitted through objects by interior mechanical stresses. Gravitational acceleration is the cause of an object's acceleration in relation to free fall.

The Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.

In astrodynamics and aerospace, a delta-v budget is an estimate of the total change in velocity (delta-v) required for a space mission. It is calculated as the sum of the delta-v required to perform each propulsive maneuver needed during the mission. As input to the Tsiolkovsky rocket equation, it determines how much propellant is required for a vehicle of given mass and propulsion system.
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft. For spacecraft far from Earth an orbital maneuver is called a deep-space maneuver (DSM).

Artificial gravity is the creation of an inertial force that mimics the effects of a gravitational force, usually by rotation. Artificial gravity, or rotational gravity, is thus the appearance of a centrifugal force in a rotating frame of reference, as opposed to the force experienced in linear acceleration, which by the equivalence principle is indistinguishable from gravity. In a more general sense, "artificial gravity" may also refer to the effect of linear acceleration, e.g. by means of a rocket engine.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
A momentum exchange tether is a kind of space tether that could theoretically be used as a launch system, or to change spacecraft orbits. Momentum exchange tethers create a controlled force on the end-masses of the system due to the pseudo-force known as centrifugal force. While the tether system rotates, the objects on either end of the tether will experience continuous acceleration; the magnitude of the acceleration depends on the length of the tether and the rotation rate. Momentum exchange occurs when an end body is released during the rotation. The transfer of momentum to the released object will cause the rotating tether to lose energy, and thus lose velocity and altitude. However, using electrodynamic tether thrusting, or ion propulsion the system can then re-boost itself with little or no expenditure of consumable reaction mass.
This is an alphabetical list of articles pertaining specifically to aerospace engineering. For a broad overview of engineering, see List of engineering topics. For biographies, see List of engineers.
A reaction engine is an engine or motor that produces thrust by expelling reaction mass, in accordance with Newton's third law of motion. This law of motion is commonly paraphrased as: "For every action force there is an equal, but opposite, reaction force."
A gravity turn or zero-lift turn is a maneuver used in launching a spacecraft into, or descending from, an orbit around a celestial body such as a planet or a moon. It is a trajectory optimization that uses gravity to steer the vehicle onto its desired trajectory. It offers two main advantages over a trajectory controlled solely through the vehicle's own thrust. First, the thrust is not used to change the spacecraft's direction, so more of it is used to accelerate the vehicle into orbit. Second, and more importantly, during the initial ascent phase the vehicle can maintain low or even zero angle of attack. This minimizes transverse aerodynamic stress on the launch vehicle, allowing for a lighter launch vehicle.

In astronautics, a powered flyby, or Oberth maneuver, is a maneuver in which a spacecraft falls into a gravitational well and then uses its engines to further accelerate as it is falling, thereby achieving additional speed. The resulting maneuver is a more efficient way to gain kinetic energy than applying the same impulse outside of a gravitational well. The gain in efficiency is explained by the Oberth effect, wherein the use of a reaction engine at higher speeds generates a greater change in mechanical energy than its use at lower speeds. In practical terms, this means that the most energy-efficient method for a spacecraft to burn its fuel is at the lowest possible orbital periapsis, when its orbital velocity is greatest. In some cases, it is even worth spending fuel on slowing the spacecraft into a gravity well to take advantage of the efficiencies of the Oberth effect. The maneuver and effect are named after the person who first described them in 1927, Hermann Oberth, an Austro-Hungarian-born German physicist and a founder of modern rocketry.
This glossary of aerospace engineering terms pertains specifically to aerospace engineering, its sub-disciplines, and related fields including aviation and aeronautics. For a broad overview of engineering, see glossary of engineering.













