
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the modulation or envelope of the wave—propagates through space.

The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.

In optics, and by analogy other branches of physics dealing with wave propagation, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.

In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the phase velocity and group velocity of waves in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency dependence of wave propagation and attenuation.
Plasma oscillations, also known as Langmuir waves, are rapid oscillations of the electron density in conducting media such as plasmas or metals in the ultraviolet region. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency only depends weakly on the wavelength of the oscillation. The quasiparticle resulting from the quantization of these oscillations is the plasmon.
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond or less. Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. Amplification of ultrashort pulses almost always requires the technique of chirped pulse amplification, in order to avoid damage to the gain medium of the amplifier.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.
Self-phase modulation (SPM) is a nonlinear optical effect of light–matter interaction. An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect. This variation in refractive index will produce a phase shift in the pulse, leading to a change of the pulse's frequency spectrum.
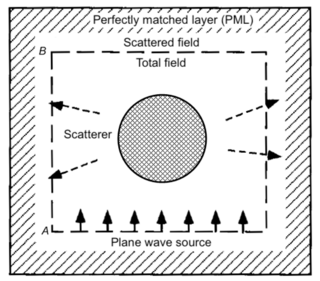
A perfectly matched layer (PML) is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FE methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
Multiphoton intrapulse interference phase scan (MIIPS) is a method used in ultrashort laser technology that simultaneously measures, and compensates femtosecond laser pulses using an adaptive pulse shaper. When an ultrashort laser pulse reaches a duration of less than a few hundred femtosecond, it becomes critical to characterize its duration, its temporal intensity curve, or its electric field as a function of time. Classical photodetectors measuring the intensity of light are still too slow to allow for a direct measurement, even with the fastest photodiodes or streak cameras.
In optics, the term soliton is used to refer to any optical field that does not change during propagation because of a delicate balance between nonlinear and linear effects in the medium. There are two main kinds of solitons:

The Nakagami distribution or the Nakagami-m distribution is a probability distribution related to the gamma distribution. The family of Nakagami distributions has two parameters: a shape parameter and a second parameter controlling spread .

Self-focusing is a non-linear optical process induced by the change in refractive index of materials exposed to intense electromagnetic radiation. A medium whose refractive index increases with the electric field intensity acts as a focusing lens for an electromagnetic wave characterized by an initial transverse intensity gradient, as in a laser beam. The peak intensity of the self-focused region keeps increasing as the wave travels through the medium, until defocusing effects or medium damage interrupt this process. Self-focusing of light was discovered by Gurgen Askaryan.
The McCumber relation is a relationship between the effective cross-sections of absorption and emission of light in the physics of solid-state lasers. It is named after Dean McCumber, who proposed the relationship in 1964.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
Precursors are characteristic wave patterns caused by dispersion of an impulse's frequency components as it propagates through a medium. Classically, precursors precede the main signal, although in certain situations they may also follow it. Precursor phenomena exist for all types of waves, as their appearance is only predicated on the prominence of dispersion effects in a given mode of wave propagation. This non-specificity has been confirmed by the observation of precursor patterns in different types of electromagnetic radiation as well as in fluid surface waves and seismic waves.
A Sverdrup wave is a wave in the ocean, or large lakes, which is affected by gravity and Earth's rotation.
The Vanna–Volga method is a mathematical tool used in finance. It is a technique for pricing first-generation exotic options in foreign exchange market (FX) derivatives.





































