H-derivative

Last updated October 02, 2024

In mathematics, the H-derivative is a notion of derivative in the study of abstract Wiener spaces and the Malliavin calculus.^[1]

Definition

Let $i:H\to E$ be an abstract Wiener space, and suppose that $F:E\to \mathbb {R}$ is differentiable. Then the Fréchet derivative is a map

\mathrm {D} F:E\to \mathrm {Lin} (E;\mathbb {R} )

;

i.e., for $x\in E$ , $\mathrm {D} F(x)$ is an element of $E^{*}$ , the dual space to $E$ .

Therefore, define the $H$ -derivative $\mathrm {D} _{H}F$ at $x\in E$ by

\mathrm {D} _{H}F(x):=\mathrm {D} F(x)\circ i:H\to \mathbb {R}

,

a continuous linear map on $H$ .

Define the $H$ -gradient $\nabla _{H}F:E\to H$ by

\langle \nabla _{H}F(x),h\rangle _{H}=\left(\mathrm {D} _{H}F\right)(x)(h)=\lim _{t\to 0}{\frac {F(x+ti(h))-F(x)}{t}}

.

That is, if $j:E^{*}\to H$ denotes the adjoint of $i:H\to E$ , we have $\nabla _{H}F(x):=j\left(\mathrm {D} F(x)\right)$ .

Related Research Articles

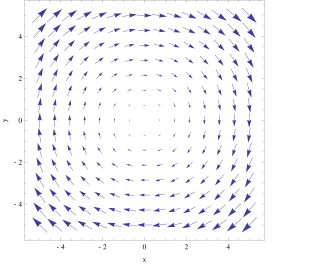
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.

In mathematics, the derivative is a fundamental tool that quantifies the sensitivity of change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation.

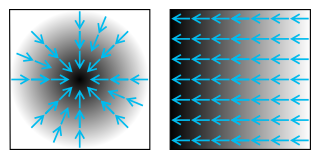
<span class="mw-page-title-main">Gradient</span> Multivariate derivative (mathematics)

In vector calculus, the gradient of a scalar-valued differentiable function $of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point, the direction of the gradient is the direction in which the function increases most quickly from, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:$

In vector calculus and differential geometry the generalized Stokes theorem, also called the Stokes–Cartan theorem, is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. In particular, the fundamental theorem of calculus is the special case where the manifold is a line segment, Green’s theorem and Stokes' theorem are the cases of a surface in $or and the divergence theorem is the case of a volume in Hence, the theorem is sometimes referred to as the fundamental theorem of multivariate calculus .$

In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In mathematics, and especially differential geometry and gauge theory, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. The most common case is that of a linear connection on a vector bundle, for which the notion of parallel transport must be linear. A linear connection is equivalently specified by a covariant derivative, an operator that differentiates sections of the bundle along tangent directions in the base manifold, in such a way that parallel sections have derivative zero. Linear connections generalize, to arbitrary vector bundles, the Levi-Civita connection on the tangent bundle of a pseudo-Riemannian manifold, which gives a standard way to differentiate vector fields. Nonlinear connections generalize this concept to bundles whose fibers are not necessarily linear.

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.

In probability theory and related fields, Malliavin calculus is a set of mathematical techniques and ideas that extend the mathematical field of calculus of variations from deterministic functions to stochastic processes. In particular, it allows the computation of derivatives of random variables. Malliavin calculus is also called the stochastic calculus of variations. P. Malliavin first initiated the calculus on infinite dimensional space. Then, the significant contributors such as S. Kusuoka, D. Stroock, J-M. Bismut, Shinzo Watanabe, I. Shigekawa, and so on finally completed the foundations.

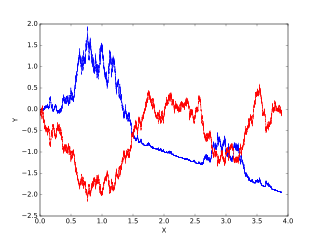
<span class="mw-page-title-main">Itô calculus</span> Calculus of stochastic differential equations

Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.

In mathematics, the derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, geometry, etc.

In mathematics, the Cameron–Martin theorem or Cameron–Martin formula is a theorem of measure theory that describes how abstract Wiener measure changes under translation by certain elements of the Cameron–Martin Hilbert space.

The concept of an abstract Wiener space is a mathematical construction developed by Leonard Gross to understand the structure of Gaussian measures on infinite-dimensional spaces. The construction emphasizes the fundamental role played by the Cameron–Martin space. The classical Wiener space is the prototypical example.

In mathematics, the Clark–Ocone theorem is a theorem of stochastic analysis. It expresses the value of some function F defined on the classical Wiener space of continuous paths starting at the origin as the sum of its mean value and an Itô integral with respect to that path. It is named after the contributions of mathematicians J.M.C. Clark (1970), Daniel Ocone (1984) and U.G. Haussmann (1978).

In mathematics, the Malliavin derivative is a notion of derivative in the Malliavin calculus. Intuitively, it is the notion of derivative appropriate to paths in classical Wiener space, which are "usually" not differentiable in the usual sense.

In mathematics, the Ornstein–Uhlenbeck operator is a generalization of the Laplace operator to an infinite-dimensional setting. The Ornstein–Uhlenbeck operator plays a significant role in the Malliavin calculus.

In mathematics, the Skorokhod integral, also named Hitsuda–Skorokhod integral, often denoted $, is an operator of great importance in the theory of stochastic processes. It is named after the Ukrainian mathematician Anatoliy Skorokhod and Japanese mathematician Masuyuki Hitsuda. Part of its importance is that it unifies several concepts:$

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on $. Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence:$

In probability theory, a branch of mathematics, white noise analysis, otherwise known as Hida calculus, is a framework for infinite-dimensional and stochastic calculus, based on the Gaussian white noise probability space, to be compared with Malliavin calculus based on the Wiener process. It was initiated by Takeyuki Hida in his 1975 Carleton Mathematical Lecture Notes.

In mathematics, calculus on Euclidean space is a generalization of calculus of functions in one or several variables to calculus of functions on Euclidean space $as well as a finite-dimensional real vector space. This calculus is also known as advanced calculus, especially in the United States. It is similar to multivariable calculus but is somewhat more sophisticated in that it uses linear algebra more extensively and covers some concepts from differential geometry such as differential forms and Stokes' formula in terms of differential forms. This extensive use of linear algebra also allows a natural generalization of multivariable calculus to calculus on Banach spaces or topological vector spaces.$

In functional analysis and measure theory, a differentiable measure is a measure that has a notion of a derivative. The theory of differentiable measure was introduced by Russian mathematician Sergei Fomin and proposed at the International Congress of Mathematicians in 1966 in Moscow as an infinite-dimensional analog of the theory of distributions. Besides the notion of a derivative of a measure by Sergei Fomin there exists also one by Anatoliy Skorokhod, one by Sergio Albeverio and Raphael Høegh-Krohn, and one by Oleg Smolyanov and Heinrich von Weizsäcker.

References

↑ Victor Kac; Pokman Cheung (2002). Quantum Calculus. New York: Springer. pp. 80–84. doi:10.1007/978-1-4613-0071-7. ISBN 978-1-4613-0071-7.

This probability-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Victor Kac; Pokman Cheung (2002). Quantum Calculus. New York: Springer. pp. 80–84. doi:10.1007/978-1-4613-0071-7. ISBN 978-1-4613-0071-7.

[1]

H-derivative

Contents

Definition

See also

Related Research Articles

References