
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.

In astronomy, seeing is the degradation of the image of an astronomical object due to turbulence in the atmosphere of Earth that may become visible as blurring, twinkling or variable distortion. The origin of this effect is rapidly changing variations of the optical refractive index along the light path from the object to the detector. Seeing is a major limitation to the angular resolution in astronomical observations with telescopes that would otherwise be limited through diffraction by the size of the telescope aperture. Today, many large scientific ground-based optical telescopes include adaptive optics to overcome seeing.

In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory to the greatest extent possible.
Phase-contrast imaging is a method of imaging that has a range of different applications. It measures differences in the refractive index of different materials to differentiate between structures under analysis. In conventional light microscopy, phase contrast can be employed to distinguish between structures of similar transparency, and to examine crystals on the basis of their double refraction. This has uses in biological, medical and geological science. In X-ray tomography, the same physical principles can be used to increase image contrast by highlighting small details of differing refractive index within structures that are otherwise uniform. In transmission electron microscopy (TEM), phase contrast enables very high resolution (HR) imaging, making it possible to distinguish features a few Angstrom apart.

In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered in the 1976 Ph.D. work of Douglas Hofstadter and is one of the early examples of modern scientific data visualization. The name reflects the fact that, as Hofstadter wrote, "the large gaps [in the graph] form a very striking pattern somewhat resembling a butterfly."

Magnetic resonance angiography (MRA) is a group of techniques based on magnetic resonance imaging (MRI) to image blood vessels. Magnetic resonance angiography is used to generate images of arteries in order to evaluate them for stenosis, occlusions, aneurysms or other abnormalities. MRA is often used to evaluate the arteries of the neck and brain, the thoracic and abdominal aorta, the renal arteries, and the legs.
In quantum mechanics, the energies of cyclotron orbits of charged particles in a uniform magnetic field are quantized to discrete values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
In special functions, a topic in mathematics, spin-weighted spherical harmonics are generalizations of the standard spherical harmonics and—like the usual spherical harmonics—are functions on the sphere. Unlike ordinary spherical harmonics, the spin-weighted harmonics are U(1) gauge fields rather than scalar fields: mathematically, they take values in a complex line bundle. The spin-weighted harmonics are organized by degree l, just like ordinary spherical harmonics, but have an additional spin weights that reflects the additional U(1) symmetry. A special basis of harmonics can be derived from the Laplace spherical harmonics Ylm, and are typically denoted by sYlm, where l and m are the usual parameters familiar from the standard Laplace spherical harmonics. In this special basis, the spin-weighted spherical harmonics appear as actual functions, because the choice of a polar axis fixes the U(1) gauge ambiguity. The spin-weighted spherical harmonics can be obtained from the standard spherical harmonics by application of spin raising and lowering operators. In particular, the spin-weighted spherical harmonics of spin weight s = 0 are simply the standard spherical harmonics:

Cardiac magnetic resonance imaging, also known as cardiovascular MRI, is a magnetic resonance imaging (MRI) technology used for non-invasive assessment of the function and structure of the cardiovascular system. Conditions in which it is performed include congenital heart disease, cardiomyopathies and valvular heart disease, diseases of the aorta such as dissection, aneurysm and coarctation, coronary heart disease. It can also be used to look at pulmonary veins.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
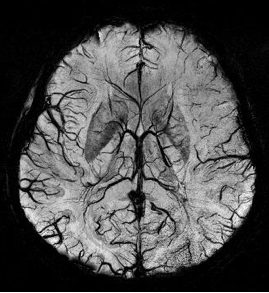
Susceptibility weighted imaging (SWI), originally called BOLD venographic imaging, is an MRI sequence that is exquisitely sensitive to venous blood, hemorrhage and iron storage. SWI uses a fully flow compensated, long echo, gradient recalled echo (GRE) pulse sequence to acquire images. This method exploits the susceptibility differences between tissues and uses the phase image to detect these differences. The magnitude and phase data are combined to produce an enhanced contrast magnitude image. The imaging of venous blood with SWI is a blood-oxygen-level dependent (BOLD) technique which is why it was referred to as BOLD venography. Due to its sensitivity to venous blood SWI is commonly used in traumatic brain injuries (TBI) and for high resolution brain venographies but has many other clinical applications. SWI is offered as a clinical package by Philips and Siemens but can be run on any manufacturer's machine at field strengths of 1.0 T, 1.5 T, 3.0 T and higher.
In the mathematical field of integral geometry, the Funk transform is an integral transform defined by integrating a function on great circles of the sphere. It was introduced by Paul Funk in 1911, based on the work of Minkowski (1904). It is closely related to the Radon transform. The original motivation for studying the Funk transform was to describe Zoll metrics on the sphere.

Real-time magnetic resonance imaging (RT-MRI) refers to the continuous monitoring ("filming") of moving objects in real time. Because MRI is based on time-consuming scanning of k-space, real-time MRI was possible only with low image quality or low temporal resolution. Using an iterative reconstruction algorithm these limitations have recently been removed: a new method for real-time MRI achieves a temporal resolution of 20 to 30 milliseconds for images with an in-plane resolution of 1.5 to 2.0 mm. Real-time MRI promises to add important information about diseases of the joints and the heart. In many cases MRI examinations may become easier and more comfortable for patients.

Cardiac magnetic resonance imaging perfusion, also known as stress CMR perfusion, is a clinical magnetic resonance imaging test performed on patients with known or suspected coronary artery disease to determine if there are perfusion defects in the myocardium of the left ventricle that are caused by narrowing of one or more of the coronary arteries.

Philip Batchelor, was a Swiss-British academic in the fields of mathematics and medical imaging.
In statistics, kernel Fisher discriminant analysis (KFD), also known as generalized discriminant analysis and kernel discriminant analysis, is a kernelized version of linear discriminant analysis (LDA). It is named after Ronald Fisher.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
The assessment of the regional function of the heart is a good tool for early detection of deterioration in certain parts of the heart wall before a cardiac arrest is diagnosed. One of the most accurate measures of changes in regional function is the use of strain as a measure of the regional function of cardiac muscle.
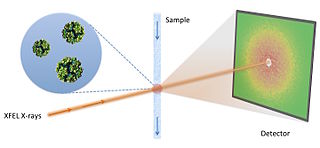
Fluctuation X-ray scattering (FXS) is an X-ray scattering technique similar to small-angle X-ray scattering (SAXS), but is performed using X-ray exposures below sample rotational diffusion times. This technique, ideally performed with an ultra-bright X-ray light source, such as a free electron laser, results in data containing significantly more information as compared to traditional scattering methods.

Phase contrast magnetic resonance imaging (PC-MRI) is a specific type of magnetic resonance imaging used primarily to determine flow velocities. PC-MRI can be considered a method of Magnetic Resonance Velocimetry. It also provides a method of magnetic resonance angiography. Since modern PC-MRI is typically time-resolved, it provides a means of 4D imaging.































