In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

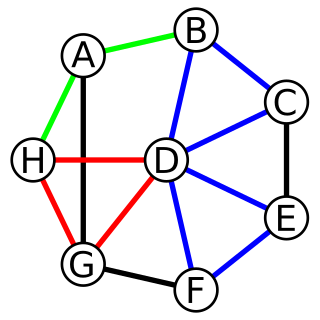
In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union. That is, the family of cographs is the smallest class of graphs that includes K1 and is closed under complementation and disjoint union.

In graph theory, the hypercube graphQn is the graph formed from the vertices and edges of an n-dimensional hypercube. For instance, the cube graph Q3 is the graph formed by the 8 vertices and 12 edges of a three-dimensional cube. Qn has 2n vertices, 2n – 1n edges, and is a regular graph with n edges touching each vertex.

In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
In the mathematical field of graph theory, the Fibonacci cubes or Fibonacci networks are a family of undirected graphs with rich recursive properties derived from its origin in number theory. Mathematically they are similar to the hypercube graphs, but with a Fibonacci number of vertices. Fibonacci cubes were first explicitly defined in Hsu (1993) in the context of interconnection topologies for connecting parallel or distributed systems. They have also been applied in chemical graph theory.

In the mathematical field of graph theory, the odd graphs are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
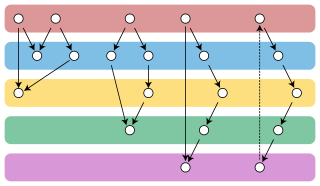
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph equals one plus the length of a longest path in an orientation of chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.

In graph theory, a path in an edge-colored graph is said to be rainbow if no color repeats on it. A graph is said to be rainbow-connected if there is a rainbow path between each pair of its vertices. If there is a rainbow shortest path between each pair of vertices, the graph is said to be strongly rainbow-connected.

In graph theory, a branch of mathematics, a radio coloring of an undirected graph is a form of graph coloring in which one assigns positive integer labels to the graphs such that the labels of adjacent vertices differ by at least two, and the labels of vertices at distance two from each other differ by at least one. Radio coloring was first studied by Griggs & Yeh (1992), under a different name, L(2,1)-labeling. It was called radio coloring by Frank Harary because it models the problem of channel assignment in radio broadcasting, while avoiding electromagnetic interference between radio stations that are near each other both in the graph and in their assigned channel frequencies.
In graph theory, a L(h, k)-labelling, L(h, k)-coloring or sometimes L(p, q)-coloring is a (proper) vertex coloring in which every pair of adjacent vertices has color numbers that differ by at least h, and any nodes connected by a 2 length path have their colors differ by at least k. The parameters, h and k are understood to be non-negative integers.

L(2, 1)-coloring is a particular case of L(h, k)-coloring. In an L(2, 1)-coloring of a graph, G, the vertices of G are assigned color numbers in such a way that adjacent vertices get labels that differ by at least two, and the vertices that are at a distance of two from each other get labels that differ by at least one.
















