In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance, and orientation. Every non-trivial rotation is determined by its axis of rotation and its angle of rotation. Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map satisfies the definition of a rotation. Owing to the above properties, the set of all rotations is a group under composition. Rotations are not commutative, making it a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable; so it is in fact a Lie group. It is compact and has dimension 3.

In Einstein's theory of general relativity, the Schwarzschild metric is the solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his much more complete and modern-looking discussion only four months after Schwarzschild.

In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.

The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.
The Schwarzschild solution describes spacetime under the influence of a massive, non-rotating, spherically symmetric object. It is considered by some to be one of the simplest and most useful solutions to the Einstein field equations.
In physics, spherically symmetric spacetimes are commonly used to obtain analytic and numerical solutions to Einstein's field equations in the presence of radially moving matter or energy. Because spherically symmetric spacetimes are by definition irrotational, they are not realistic models of black holes in nature. However, their metrics are considerably simpler than those of rotating spacetimes, making them much easier to analyze.
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.

A photon sphere or photon circle is an area or region of space where gravity is so strong that photons are forced to travel in orbits. The radius of the photon sphere, which is also the lower bound for any stable orbit, is, for a Schwarzschild black hole:

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. As with the rest of analytical mechanics, Routhian mechanics is completely equivalent to Newtonian mechanics, all other formulations of classical mechanics, and introduces no new physics. It offers an alternative way to solve mechanical problems.
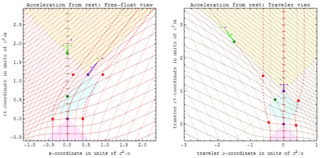
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is thus acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured. Gravitation therefore does not cause proper acceleration, since gravity acts upon the inertial observer that any proper acceleration must depart from. A corollary is that all inertial observers always have a proper acceleration of zero.
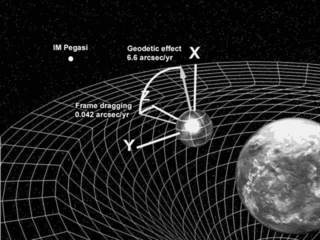
The geodetic effect represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.
In astrophysics, the Tolman–Oppenheimer–Volkoff (TOV) equation constrains the structure of a spherically symmetric body of isotropic material which is in static gravitational equilibrium, as modelled by general relativity. The equation is
Gullstrand–Painlevé coordinates are a particular set of coordinates for the Schwarzschild metric – a solution to the Einstein field equations which describes a black hole. The ingoing coordinates are such that the time coordinate follows the proper time of a free-falling observer who starts from far away at zero velocity, and the spatial slices are flat. There is no coordinate singularity at the Schwarzschild radius. The outgoing ones are simply the time reverse of ingoing coordinates.
In general relativity, Lense–Thirring precession or the Lense–Thirring effect is a relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is a gravitomagnetic frame-dragging effect. It is a prediction of general relativity consisting of secular precessions of the longitude of the ascending node and the argument of pericenter of a test particle freely orbiting a central spinning mass endowed with angular momentum .

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is adapted to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented.
Multipole radiation is a theoretical framework for the description of electromagnetic or gravitational radiation from time-dependent distributions of distant sources. These tools are applied to physical phenomena which occur at a variety of length scales - from gravitational waves due to galaxy collisions to gamma radiation resulting from nuclear decay. Multipole radiation is analyzed using similar multipole expansion techniques that describe fields from static sources, however there are important differences in the details of the analysis because multipole radiation fields behave quite differently from static fields. This article is primarily concerned with electromagnetic multipole radiation, although the treatment of gravitational waves is similar.
In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.
The near-horizon metric (NHM) refers to the near-horizon limit of the global metric of a black hole. NHMs play an important role in studying the geometry and topology of black holes, but are only well defined for extremal black holes. NHMs are expressed in Gaussian null coordinates, and one important property is that the dependence on the coordinate is fixed in the near-horizon limit.











