The Hausdorff medal is a mathematical prize awarded every two years by the European Set Theory Society. The award recognises the work considered to have had the most impact within set theory among all articles published in the previous five years. The award is named after the German mathematician Felix Hausdorff (1868–1942).
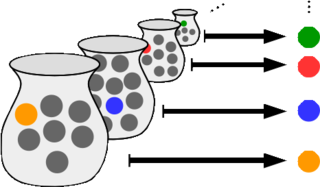
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.
In mathematics, specifically set theory, the continuum hypothesis is a hypothesis about the possible sizes of infinite sets. It states:
"There is no set whose cardinality is strictly between that of the integers and the real numbers."
Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics.
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX. The Stone–Čech compactification βX of a topological space X is the largest, most general compact Hausdorff space "generated" by X, in the sense that any continuous map from X to a compact Hausdorff space factors through βX. If X is a Tychonoff space then the map from X to its image in βX is a homeomorphism, so X can be thought of as a (dense) subspace of βX; every other compact Hausdorff space that densely contains X is a quotient of βX. For general topological spaces X, the map from X to βX need not be injective.

Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.
In the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large". The proposition that such cardinals exist cannot be proved in the most common axiomatization of set theory, namely ZFC, and such propositions can be viewed as ways of measuring how "much", beyond ZFC, one needs to assume to be able to prove certain desired results. In other words, they can be seen, in Dana Scott's phrase, as quantifying the fact "that if you want more you have to assume more".

William Hugh Woodin is an American mathematician and set theorist at Harvard University. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinals, the Woodin cardinals, bears his name. In 2023, he was elected to the National Academy of Sciences.

John Robert Steel is an American set theorist at University of California, Berkeley. He has made many contributions to the theory of inner models and determinacy. With Donald A. Martin, he proved projective determinacy, assuming the existence of sufficient large cardinals. He earned his Ph.D. in Logic & the Methodology of Science at Berkeley in 1977 under the joint supervision of John West Addison Jr. and Stephen G. Simpson.
Determinacy is a subfield of set theory, a branch of mathematics, that examines the conditions under which one or the other player of a game has a winning strategy, and the consequences of the existence of such strategies. Alternatively and similarly, "determinacy" is the property of a game whereby such a strategy exists. Determinacy was introduced by Gale and Stewart in 1950, under the name "determinateness".

Matthew Dean Foreman is an American mathematician at University of California, Irvine. He has made notable contributions in set theory and in ergodic theory.
In the mathematical field of set theory, the proper forcing axiom (PFA) is a significant strengthening of Martin's axiom, where forcings with the countable chain condition (ccc) are replaced by proper forcings.
In set theory, Ω-logic is an infinitary logic and deductive system proposed by W. Hugh Woodin as part of an attempt to generalize the theory of determinacy of pointclasses to cover the structure . Just as the axiom of projective determinacy yields a canonical theory of , he sought to find axioms that would give a canonical theory for the larger structure. The theory he developed involves a controversial argument that the continuum hypothesis is false.
In the mathematical field of set theory, the Solovay model is a model constructed by Robert M. Solovay in which all of the axioms of Zermelo–Fraenkel set theory (ZF) hold, exclusive of the axiom of choice, but in which all sets of real numbers are Lebesgue measurable. The construction relies on the existence of an inaccessible cardinal.
In mathematical set theory, the Mitchell order is a well-founded preorder on the set of normal measures on a measurable cardinal κ. It is named for William Mitchell. We say that M ◅ N if M is in the ultrapower model defined by N. Intuitively, this means that M is a weaker measure than N.

Joel David Hamkins is an American mathematician and philosopher who is the John Cardinal O'Hara Professor of Logic at the University of Notre Dame. He has made contributions in mathematical and philosophical logic, set theory and philosophy of set theory, in computability theory, and in group theory.
The Higher Infinite: Large Cardinals in Set Theory from their Beginnings is a monograph in set theory by Akihiro Kanamori, concerning the history and theory of large cardinals, infinite sets characterized by such strong properties that their existence cannot be proven in Zermelo–Fraenkel set theory (ZFC). This book was published in 1994 by Springer-Verlag in their series Perspectives in Mathematical Logic, with a second edition in 2003 in their Springer Monographs in Mathematics series, and a paperback reprint of the second edition in 2009 (ISBN 978-3-540-88866-6).
Itay Neeman is a set theorist working as a professor of mathematics at the University of California, Los Angeles. He has made major contributions to the theory of inner models, determinacy and forcing.